Яков Кротов. Владимир Уваров о календарной реформе Цезаря и Евангелии

С любезного разрешения автора перенесено с сайта: http://www.hrono.ru/statii/2007/revs.html

Автор о себе:

Я, Уваров Владимир Анатольевич, родился 24 января 1951 года в городе Ульяновске. В 1974 году закончил кафедру физики элементарных частиц физического факультета МГУ им. М.В. Ломоносова. После окончания университета и по настоящее время работаю в Институте Физики Высоких Энергий (город Протвино Московской области). Должность - ведущий научный сотрудник, учёная степень - доктор физико-математических наук. Теорией и историей календарей увлекаюсь с детства. Женат, имею двух сыновей, внука и внучку.

1. Введение

Несмотря на то, что солнечный григорианский календарь (новый стиль) уже давно официально введён в большинстве стран мира, до сих пор некоторые религиозные праздники, такие, например, как Пасха, отмечаются по древним лунно-солнечным календарям. Этим, однако, роль древних календарей не ограничивается: они представляют исключительную ценность для хронологических исследований.

Одной из давно известных проблем, относящейся к хронологии библейских событий, является датировка Тайной вечери — последней трапезы Иисуса Христа с апостолами. Эта проблема напрямую связана с вопросом: была ли Тайная вечеря именно пасхальной трапезой. Так, из слов первых трёх канонических евангелистов Матфея, Марка и Луки следует, что Тайная вечеря состоялась вечером с 14-го на 15-е нисана, когда уже наступило время ветхозаветной пасхи, но четвёртый евангелист Иоанн определённо указывает на предыдущий вечер — на вечер с 13-го на 14-е нисана, когда время ветхозаветной пасхи ещё не наступило. На протяжении вот уже почти 20-ти веков было сделано немало остроумных попыток решить эту проблему. Однако ни одна из них не привела к общепризнанному «единственному» объяснению. Тем не менее, в настоящей статье предпринята ещё одна попытка согласовать очевидное противоречие в свидетельствах евангелистов. Эта попытка основывается на изложенном ниже детальном анализе исторически известных календарных принципов I в. до н.э. Напомним некоторые из них (см. книги [1–3]).

Астрономической основой солнечного календаря является солнечный (тропический) год, определяемый как средний промежуток времени между двумя последовательными прохождениями центра Солнца через точку весеннего равноденствия, а лунно-солнечного — ещё и лунный (синодический) месяц, определяемый как средний промежуток времени между двумя последовательными одинаковыми фазами Луны. Точкой весеннего равноденствия называется та точка эклиптики — пути видимого годичного движения центра Солнца на небесной сфере среди звёзд, в которой Солнце пересекает небесный экватор и переходит из южного полушария в северное. По современным данным длина тропического года составляет 365,242199 суток, а длина синодического месяца — 29,530588 суток.

Один из первых солнечных календарей зародился в Древнем Египте в долине реки Нил. Ежегодные разливы Нила для древних египтян имели жизненно важное значение, так как именно от них зависел урожай основных злаковых культур. Чтобы заблаговременно начать земледельческие работы, древние египтяне, оценивая промежуток времени между этими разливами, вначале определили длину года в 360 дней и разделили год на 12 равных месяцев, каждый из которых содержал по 30 дней. В дальнейшем длина года была увеличена до 365-ти дней, но дополнительные пять дней не были прибавлены ни к одному из месяцев года, а были добавлены в конец года как «сверхгодичные». В III в. до н.э. была предпринята попытка ввести в этот календарь високосный год, т.е. добавлять раз в четыре года ещё один (шестой) «сверхгодичный» день. Однако такая реформа была введена в жизнь лишь в 26 г. до н.э., когда Египет, столицей которого в то время была Александрия — научный центр древнего мира, оказался под властью римского императора Августа. Начиная с этого времени «стабильный египетский» (александрийский) календарь идёт синхронно с солнечным юлианским (старым стилем): начало александрийского года — 1-е тота — приходится на 29-е августа, а високосный день вставляется на полгода раньше, чем в юлианском календаре (в этом случае 1-е тота приходится на 30-е августа).

Древнеримский календарь, сложившийся к середине I в. до н.э., имел некое подобие лунно-солнечного календаря. Его год длиной в 355 дней (близкой к 354,37 дням, т.е. к длине 12-ти синодических месяцев) состоял из 12-ти календарных месяцев, длины которых чередовались следующим образом:

Первым месяцем года был 31-дневный март. Чтобы держать начало года вблизи одного и того же сезона, римляне в каждом втором году «вклинивали» в последний месяц года, т.е. в 28-дневный февраль (между 23-м и 24-м днями), вставочный месяц длиной попеременно в 22 или 23 дня, причём один раз в 24 года вставка 23-дневного месяца не проводилась. Такую привязку календаря к движению как Луны, так и Солнца можно назвать достаточно примитивной. Кроме того, начиная со II в. до н.э. римские жрецы получили право «назначать для вставочного месяца столько дней, сколько потребуется», что привело к хаотичности календаря и к необходимости его реформы. В 46 г. до н.э. римский верховный жрец Юлий Цезарь, который до этого побывал в Египте и познакомился с египетским солнечным календарём, поручил создание нового календаря группе александрийских астрономов во главе с Созигеном.

С 1-го января (по ст.ст.) 45 г. до н.э. новым римским (юлианским) календарём стал солнечный календарь с длиной года в 365 дней, а один раз в четыре года — в 366 дней. Юлианский год был разделён Созигеном на 12 месяцев, первым из которых стал январь. Число дней в месяцах было упорядочено по принципу: все нечётные месяцы имели по 31 день, а чётные — по 30, за исключением февраля простого года, который содержал 29 дней. Високосный день (также как раньше вставочный месяц) был «спрятан» между 23-м и 24-м днями февраля и получил название «второе 24-е февраля». В честь Юлия Цезаря месяц квинтилис в 44 г. до н.э. был переименован в июль. Вскоре, однако, римские жрецы вновь запутали календарь, объявляя високосным каждый третий год календаря. Эту ошибку исправил император Август, так что начиная с 1-го марта 4 г. н.э. юлианский календарь начал функционировать нормально. В честь императора Августа месяц секстилис был переименован в август. Длина этого месяца была установлена юлианской реформой в 30 дней. Однако посчитали неудобным оставить в месяце, посвящённом Августу, меньше дней, чем в месяце, посвящённом Цезарю. Поэтому к августу добавили один день, отняв его от февраля. Но теперь получилось, что три месяца подряд (июль, август и сентябрь) имеют по 31 день. Поэтому один день сентября перенесли на октябрь, а один день ноября — на декабрь. Тем самым было нарушено изначальное созигеновское правило чередования длинных и коротких месяцев, введённое Цезарем.

С глубокой древности многие народы «по обычаям предков», чтобы «сохранять в годах согласие с Солнцем, а в днях и месяцах — с Луной», при определении дат своих праздников пользовались лунно-солнечными календарями. Родиной таких календарей (сначала лунных, а затем и лунно-солнечных) следует признать Древний Вавилон на юге Месопотамской равнины (Междуречья Тигра и Евфрата). В своё время Древний Вавилон был культурным и научным центром всего Ближнего Востока, а вавилонский календарь послужил прообразом при разработке календарных систем у многих других народов Передней Азии. Что же касается Древнего Египта, то в IV в. до н.э. Александр Македонский «принёс» туда македонский лунно-солнечный календарь, который стал там использоваться параллельно с солнечным календарём главным образом для культовых целей.

Начало месяца в лунно-солнечных календарях подгонялось как можно ближе к новолунию. Длина лунного (синодического) месяца, равная примерно 29,53 суткам, определяла длину календарного месяца в 29 или 30 дней. Из численного соотношения между длинами лунного месяца и солнечного года следует, что 12 лунных месяцев короче солнечного года примерно на 11 дней, а 13 лунных месяцев длиннее солнечного года примерно на 19 дней. Поэтому для привязки лунно-солнечных календарей к временам года один раз в два-три года вставлялся 13-й (эмболисмический) месяц. В V в. до н.э. древнегреческий астроном Метон установил следующее соотношение (так называемый метонов цикл):

которое послужило основой для построения многих лунно-солнечных календарей и справедливо считается одним из шедевров греческой астрономии. Начиная с конца IV в. до н.э. 19-летний цикл несомненно использовался в вавилонском лунно-солнечном календаре со вставкой эмболисмических месяцев в 3-м, 6-м, 8-м, 11-м, 14-м, 17-м и 19-м годах цикла. Год в лунно-солнечных календарях начинался, как правило, в дни около равноденствий или солнцестояний. Так, в вавилонском календаре начало года удерживалось вблизи весеннего равноденствия, а в сирийско-македонском — вблизи осеннего. По некоторым данным, первоначально древние греки начинали свой год вблизи зимнего солнцестояния, но потом — вблизи летнего.

2. Первичное расписание новолуний в юлианском календаре

По совету Созигена Александрийского Юлий Цезарь отказался от лунно-солнечного календаря и ввёл солнечный. Значит ли это, что римляне перестали интересоваться столь чтимым ими ранее новолунием? Есть два исторически известных факта, которые позволяют усомниться в утвердительном ответе на данный вопрос.

Во-первых, по сообщениям греческого писателя Макробия (V в. н.э.) первый день юлианского календаря — 1-е января 45 г. до н.э. — совпал с первым новолунием после зимнего солнцестояния. «Несомненно, это было сделано с умыслом — для удобства расчётов фаз Луны, которые (возможно, на основании метонова цикла) были будто бы "расписаны" по числам месяцев календаря» [1, с.117].

Во-вторых, в I в. до н.э. зимнее солнцестояние приходилось на 23−24 декабря, из чего следует, что первый день после зимнего солнцестояния — 25-е декабря — отстоит от 29-го августа, на которое после реформы 26 г. до н.э. приходится начало александрийского года — 1-е тота, ровно на четыре календарных лунных месяца (два месяца по 30 дней и два по 29). Поэтому в I в. до н.э. пятое новолуние александрийского года являлось первым после зимнего солнцестояния. Вышеприведённую фразу, сказанную И.А. Климишиным по отношению к юлианскому календарю, можно повторить и по отношению к александрийскому: несомненно, это было сделано с умыслом — для удобства расчётов фаз Луны...

К этим двум фактам можно ещё добавить и следующие утверждения из литературы. Так, А.М. Эфросман, ссылаясь на книги M.Н. Лалоша и Н.В. Степанова, пишет: «Весьма остроумное распределение 235 реальных лунных месяцев длительностью по 29 и 30 дней в 19 реальных солнечных годах по юлианскому календарю произвёл <...> египетский астроном Созиген — создатель юлианского календаря, введённого Юлием Цезарем в 46 г. до н.э.» [4, с.353]. Кроме того, будет, по-видимому, интересно заметить, что в XV в. византийский историк Георгий Плетон, обсуждая вопросы, связанные с неточностью юлианского календаря, предлагал «возвратиться к лунно-солнечному календарю с началом года от новолуния, которое приходилось бы близко к зимнему солнцестоянию» (подчёркнуто мной — В.У.) [1, с.190].

Таким образом, можно предположить, что Юлий Цезарь ввёл солнечный календарь не потому, что римляне совсем отказались от исчисления лунных фаз, а потому, что александрийские астрономы во главе с Созигеном предложили достаточно удобный способ составления расписания новолуний («лунного течения») в солнечном календаре (сначала в юлианском, а потом и в александрийском). При этом важно подчеркнуть, что имеется в виду не самостоятельный лунно-солнечный календарь, а именно расписание новолуний, жестко привязанное к солнечному календарю и не требующее никаких коррекций.

Заметим, что незадолго до своей календарной реформы Юлий Цезарь посетил все значительные города Сирии и некоторым из них даровал автономию и привилегии (речь идёт о том самом походе Юлия Цезаря из Египта в Сирию и Малую Азию в 47 г. до н.э., о котором сам Цезарь сказал: «пришёл, увидел, победил»). Поэтому можно предположить, что вскоре после этого события в честь Цезаря и было составлено «лунное течение в юлианском календаре», предназначавшееся народам восточных провинций Римской империи, которые не желали отказываться от лунно-солнечного года, и которым римское правительство не навязывало официальный юлианский календарь. Заметим также, что в западных провинциях империи юлианский календарь был введён в основном без изменений, но в восточных провинциях новое исчисление времени в отношении начала года, названий и продолжительности месяцев обычно приспосабливалось к местным обычаям [3, с.42–43].

Так какой же лунно-солнечный календарь (расписание новолуний в юлианском календаре) могли предложить александрийские астрономы в I в. до н.э.? Попробуем реконструировать этот календарь на основе вышеупомянутых фактов, имеющих прямое отношение к созданию юлианского календаря. Известно, что первый год после юлианской реформы начался в первое новолуние после зимнего солнцестояния, и что до августианской реформы нечётные юлианские месяцы были длинными, а чётные — короткими. Обобщая эти факты, можно сформулировать первые два принципа искомого лунно-солнечного календаря: 1) не только первый, но и каждый последующий лунно-солнечный год начинается в первое новолуние после зимнего солнцестояния; 2) не только юлианские, но и лунные месяцы распределены по Созигену, т.е. нечётные лунные месяцы имеют продолжительность в 30 дней, а чётные — в 29.

Далее потребуются некоторые вычисления. Согласно второму принципу, сформулированному выше для искомого календаря, 12-месячный (простой) лунно-солнечный год состоит из 6×30+6×29 = 354 дней, а 13-месячный (эмболисмический) — из 7×30+6×29 = 384. Из этого следует, что солнечный год продолжительностью в 365 дней длиннее простого лунно-солнечного года на 365−354 = 11 дней, но короче эмболисмического — на 384−365 = 19. Поэтому в юлианском календаре начало каждого лунно-солнечного года может быть вычислено по следующему простому алгоритму, который назовём «−11 или +19». Итак, первый лунно-солнечный год начнём 25-го декабря — в день самого раннего первого новолуния после зимнего солнцестояния. Каждый последующий лунно-солнечный год начнём по отношению к предыдущему либо на 11 дней раньше, либо на 19 дней позже. Сначала попробуем начать «на 11 дней раньше», но если окажется, что лунно-солнечный год начинается до 25-го декабря, то тогда начнём «на 19 дней позже».

Алгоритм «−11 или +19» справедлив для солнечного года продолжительностью в 365 дней. А как быть с високосным днём? Юлий Цезарь «спрятал» этот високосный день внутри февраля, а числа остальных дней февраля, включая последний, не изменил. Формально получилось, что февраль до августианской реформы всегда имел 29 дней, хотя в високосный год его реальная длина была 30 дней. По аналогии с этим сформулируем третий принцип искомого лунно-солнечного календаря: 3) второй принцип относится к формальной продолжительности лунного месяца, т.е. к такой продолжительности, при определении которой високосный день в расчёт не берётся. Например, пусть первый день лунного месяца попадает на 12-е февраля, а последний — на 12-е марта. Тогда в високосном году формальная продолжительность данного лунного месяца составляет 29 дней, а реальная — 30.

Чтобы реконструировать искомый лунно-солнечный календарь, осталось решить на каком «шаге» остановить алгоритм «−11 или +19», т.е. решить на сколько лет надо составить календарь, предполагая, что дальше он будет циклически повторяться. Любой цикл, полученный с помощью данного алгоритма и состоящий из N лунно-солнечных годов, характеризуется так называемым «скачком Луны», определяемым как сдвижка между юлианскими датами начала первого и начала (N+1)-го годов. Легко проверить, что нулевой «скачок Луны» получается для 30-летнего цикла. Это значит, что 31-й год, рассчитанный по алгоритму «−11 или +19», снова начнётся 25-го декабря. Поэтому 30 лет — это максимально возможная длина цикла, если, конечно, не делать сложные циклы, состоящие из нескольких подциклов. Для любого другого цикла с ненулевым «скачком» последний лунно-солнечный год автоматически укорачивается на величину этого «скачка», что приводит к нарушению в этом году порядка чередования 30- и 29-дневных месяцев, задаваемого сформулированными выше календарными принципами. Так, если «скачок Луны» равен одному дню, то в последнем году цикла один из 30-дневных месяцев становится 29-дневным; если же «скачок» больше, то и число укороченных месяцев тоже больше.

Результат первых 20-ти шагов алгоритма «−11 или +19» приведён в таблице 1, где A — номер года по порядку (шаг алгоритма), НЛСГ — юлианская дата первого новолуния после зимнего солнцестояния (начало лунно-солнечного года). Как видно из этой таблицы, «скачок Луны» в один день получился для 19-летнего цикла, а в два дня — для 8-летнего. Очевидно, что чем меньше «скачок Луны», тем «элегантнее» выглядит календарь. Поэтому ограничимся только теми циклами, в которых «скачок Луны» не превышает одного дня. Таких циклов получилось только два — 30-летний и 19-летний. Но какой именно из них могли выбрать александрийские астрономы? Для ответа на этот вопрос определим погрешности рассмотренных циклов с учётом тех астрономических данных, которые были известны в I в. до н.э.

Таблица 1 Результат реконструкции и привязки лунно-солнечных годов искомого календаря с помощью алгоритма «−11 или +19».
Обозначения: A — номер года по порядку, точкой (•) обозначены эмболисмические годы; Г — номер года по историческому счёту в интервале от 58 до 40 гг. до н.э.; L — номер года в 19-летнем цикле, в котором эмболисмические годы имеют номера 3, 6, 8, 11, 14, 17, 19; НЛСГ — юлианская дата начала лунно-солнечного года (декабрьская дата идёт перед январём года Г); EL — лунная эпакта, т.е. возраст Луны по включительному счёту на 23 января. Календарь привязан к историческому летосчислению из условия, что год A=14 совпадает с годом Г = 45 г. до н.э., в котором новолуние пришлось на 1 января.

В IV в. до н.э. древнегреческий астроном Калипп уже знал, что в 19-ти солнечных годах цикла Метона не 6940 дней, а только 6939,75. Поэтому он решил усовершенствовать цикл: число лет и число календарных лунных месяцев в его цикле были увеличены ровно в четыре раза, но число дней стало не 4×6940 = 27760, а на один день меньше, т.е. 4×6940−1 = 27759. Это значит, что средняя продолжительность солнечного года в цикле Калиппа составляет 27759:(4×19) = 365,25 дней — ту же величину, что и в юлианском календаре [2, с.104–105]. Поэтому, строго говоря, 19-летний цикл, найденный в юлианском календаре по алгоритму «−11 или +19», является не циклом Метона, а как бы скрытым циклом Калиппа (скрытым — потому, что длина цикла в годах берётся как в цикле Метона, а в днях — как в одной четверти цикла Калиппа).

Во II в. до н.э. древнегреческий астроном Гиппарх открыл явление прецессии, т.е. явление перемещения точки весеннего равноденствия по эклиптике относительно неподвижных звёзд и навстречу годичному движению Солнца, и установил, что длина солнечного (тропического) года на несколько минут короче, чем 365,25 суток. Гиппарх считал, что длину четырёх циклов Калиппа надо укоротить на один день. Тогда получилось равенство:

из которого следует, что средняя продолжительность лунного (синодического) месяца уже во времена Гиппарха была определена с высокой точностью. Значение S_^г = 111035:3760 = 29,53059 суток, найденное Гиппархом, всего лишь на 0,3 секунды отличается от принимаемого сегодня [2, с.105–106].

Теперь вернёмся к 30-летнему и 19-летнему циклам, полученным при использовании алгоритма «−11 или +19». Погрешность цикла (D) определим как разность между длиной всех календарных лунных месяцев цикла (L_^к) и длиной такого же количества реальных лунных месяцев (L_^р), т.е. D = L_^к−L_^р. В качестве средней длины реального лунного месяца возмём оценку Гиппарха (S_^г). 19-летний цикл состоит из 235 календарных лунных месяцев, поэтому L_^р = S_^г×235, L_^к = 365,25×19 и D = 1,47 часа, а 30-летний — из 371, поэтому L_^р = S_^г×371, L_^к = 365,25×30 и D = 1,65 суток. Это значит, что реальные новолуния «спешат» по отношению к расписанию новолуний в 19-летнем цикле на 1,47 часа за 19 лет, а в 30-летнем — на 1,65 суток за 30 лет. Как видно, погрешность 19-летнего цикла значительно меньше, чем погрешность 30-летнего. Поэтому вполне можно сказать, что по точности 19-летний цикл не имеет себе конкурентов.

Несколько слов о 8-летнем цикле. Этот цикл появился в VI в. до н.э. и использовался в вавилонском календаре вплоть до создания 19-летнего цикла в конце IV в. до н.э., а у греков, несмотря на открытие Метона, оставался, по свидетельству римского писателя Цензорина [1, с.188], наиболее популярным ещё и в середине III в. н.э. Важно подчеркнуть, что в тех случаях, когда использовался 8-летний цикл, лунно-солнечный календарь не был жёстко привязан к юлианскому календарю, а чтобы всё же как-то согласовывать 8-летний цикл одновременно и с Луной, и с Солнцем, календарный лунный месяц эпизодически увеличивался или уменьшался на один-два дня. Если же такие исправления в календарь не вносились, то погрешность 8-летнего цикла составляла 1,53 суток за 8 лет, что значительно хуже, чем у 19-летнего цикла.

Итак, 19-летний цикл, как бы заново открытый, оказался единственно приемлемым циклом, на котором при составлении расписания новолуний в юлианском календаре следует остановить алгоритм «−11 или +19». Однако осталось ответить на последний вопрос — какой из 30-дневных лунных месяцев последнего года цикла (с номером A=19) должен быть укорочен на один день, или, другими словами, где поместить «скачок Луны». Чтобы ответить на этот вопрос, обратимся к историческим фактам, известным в I в. до н.э. Так, в древнеримском календаре для корректировки средней длины года вставочный месяц «вклинивали» в последний месяц года, и в египетском календаре с той же самой целью «сверхгодичные» дни добавляли в конец года. По аналогии с этими фактами, александрийские астрономы также могли поместить «скачок Луны» в конец года, т.е. могли укоротить последний 30-дневный лунный месяц. Вместе с условием, что цикл начинается 25-го декабря, будем считать это четвёртым принципом искомого календаря.

Таким образом, для однозначного составления первичного расписания новолуний в юлианском календаре все принципы сформулированы. Повторим их:

Из таблицы 1 видно, что начало (первое новолуние) лунно-солнечного года с номером A=14 приходится на 1-е января. Этим можно воспользоваться для привязки искомого лунно-солнечного календаря к историческому летосчислению. Действительно, юлианский календарь, как уже отмечалось, был введён с 1-го января 45 г. до н.э. и именно в этот день было новолуние. Поэтому положим, что 45 г. до н.э. соответствует году с номером A=14, определяя, тем самым, привязку и всех остальных годов, как показано в столбце Г таблицы 1.

В вавилонском лунно-солнечном календаре начиная с конца IV в. до н.э. эмболисмический месяц вставлялся в 3-м, 6-м, 8-м, 11-м, 14-м, 17-м и 19-м годах 19-летнего лунного цикла [3, с.21]. Впоследствии это (вавилонское) распределение эмболисмических годов в цикле стало применяться во многих лунно-солнечных календарях. Заметим, что при использовании алгоритма «−11 или +19» получилось другое распределение, а именно: 13-й месяц имеют 1-й, 3-й, 6-й, 9-й, 11-й, 14-й и 17-й годы цикла (они отмечены точкой в столбце A таблицы 1). Однако, ничего не мешает эти годы цикла перенумеровать «по-вавилонски». Результат такой перенумерации показан в столбце L таблицы 1.

Одним из исторически известных вариантов 19-летнего цикла является так называемый сирийский (он же иудейский) лунный цикл, в котором порядковый номер года — круг Луны — определяется как остаток от деления на 19 числа года по нашему летосчислению, уменьшенного на 2 [1, с.119, 122]. Согласно этому правилу круг Луны для 250 г. н.э. равен 1. Отступив назад от этого года на шестнадцать 19-летних периодов, получаем 250−(16×19) = −54 год, который по историческому счёту соответствует 55 г. до н.э. (заметим, что в историческом счёте нет нулевого года). Это значит, что круг Луны для 55 г. до н.э. тоже равен 1. Сравнивая этот результат с нумерацией «по-вавилонски», приведённой в столбце L таблицы 1, можно сделать важный вывод: получилось, что L — это круг Луны в сирийском цикле.

Теперь по вышеизложенным «четырём принципам» можно составить первичное расписание новолуний в юлианском календаре. Это расписание приведено в таблице 2, в которой для нумерации годов цикла используется сирийский круг Луны. Проверим, как точно таблица 2 соответствует реальным фазам Луны в том интервале лет, который приведён в столбце Г таблицы 1, т.е. в интервале с 58-го по 40-й гг. до н.э. Поступим следующим образом: для каждого календарного лунного месяца 19-летнего цикла определим интервал времени между началом суток календарного новолуния и моментом соответствующего астрономического новолуния, затем, используя полученные величины, определим усреднённый интервал времени T_^ср. При этом, началом суток календарного новолуния будем считать полночь по александрийскому времени (время по Гринвичу плюс два часа), а даты и время астрономических новолуний возьмём из таблиц Ф. Эспенака [5], вычисленных по формулам Ж. Меёса [6].

Таблица 2 Первичное расписание новолуний в юлианском календаре, составленное по четырём календарным принципам эпохи Юлия Цезаря.
Обозначения: L — круг Луны сирийского цикла, точкой (•) обозначены эмболисмические годы; m — номер месяца в лунно-солнечном году (нечётный номер — 30-дневный месяц, чётный — 29-дневный); курсивом обозначены новолуния весенних (пасхальных) месяцев, жирным шрифтом — новолуния александрийского месяца тота, наклонным — новолуние нечётного, но 29-дневного месяца, т.е. месяца «скачка Луны».

Однако сначала сравним таблицу новолуний, составленную Ф. Эспенаком, с известной таблицей «астрономических новолуний (605 г. до н.э. — 308 г. н.э.)», опубликованной Ф.К. Гинцелем в 1906 и 1911 гг., а также приведённой в книге Э. Бикермана [3, с.108–159]. Разность между моментами времени новолуния из таблицы Гинцеля (ТГ) и того же самого новолуния из таблицы Эспенака (ТЭ), усреднённая по всем новолуниям 19-летнего периода с 58-го по 40-й гг. до н.э., составляет ТГ−ТЭ = 18 мин, что несущественно для приводимых ниже выводов.

Расчёт показывает, что средний момент астрономического новолуния в 58–40 гг. до н.э. приходился на день календарного (из таблицы 2) новолуния на 6 час 9 мин утра по александрийскому времени. Заметим, что в Древнем Египте сутки в солнечном календаре определённо начинались утром на рассвете [3, с.11], что, по-видимому, относится и к началу египетского лунного месяца [3, с.36]. Вопрос же о начале суток в древнеримском календаре представляется спорным, однако стоит отметить, что по свидетельству древнеримского политика и философа Марка Туллия Цицерона (I в. до н.э.) «сутки у римлян будто бы начинались с утра» [1, с.281]. На основании всего вышеизложенного можно сделать важный вывод, что с точки зрения александрийских астрономов I в. до н.э. реконструированное расписание новолуний в юлианском календаре достаточно точно согласуется с реальными лунными фазами: средний момент астрономического новолуния совпадает с началом «по-египетски» первых суток календарного лунного месяца.

Известно, что у многих народов Римской империи сутки начинались не утром на рассвете, как у египтян, а вечером на закате. Поэтому отмеченная выше «привязка по-египетски» календарных лунных месяцев к фазам Луны, скорее всего, для этих народов не подходила. В связи с этим, однако, уместно вспомнить об «ошибке» римских жрецов, которые в течение 36-ти лет после смерти Юлия Цезаря (с 44-го по 9-й гг. до н.э.) вставили в юлианский календарь три лишних високосных дня, из-за чего в следующие 12 лет (с 8 г. до н.э. по 4 г. н.э.), в течение которых должно было быть три високосных дня, по распоряжению императора Августа не было ни одного. Поэтому в последнюю треть I в. до н.э. приведённые в таблице 2 даты новолуний приходились в «неправильном» юлианском календаре на один-три дня позже, чем в «правильном», т.е. на один-три дня позже соответствующих астрономических новолуний. Это значит, что даты новолуний в «неправильном» календаре чаще всего были датами первого появления лунного серпа на вечернем небе (конечно, при благоприятных погодных условиях). Таким образом, в первое время после календарной реформы благодаря «ошибке» римских жрецов «привязка по-египетски» не могла быть препятствием для возможного распространения реконструированного «лунного течения» среди тех народов империи, которые начинали свои лунные месяцы на закате при первом появлении молодой Луны.

Далее, любопытным и определённо заслуживающим упоминания является тот факт, что промежуток времени между 29-м августа (1-м тота — началом александрийского года) и 25-м декабря (первым днём после зимнего солнцестояния в I в. до н.э.) составляет ровно четыре календарных лунных месяца. Действительно, в календаре, приведённом в таблице 2, все четвёртые новолуния от конца лунно-солнечного года (выделенные жирным шрифтом) попадают в интервал от 30-го августа до 27-го сентября включительно, т.е. на александрийский месяц тот. Этот месяц, когда он идёт сразу же после високосного александрийского года, соответствует интервалу от 30-го августа до 28-го сентября, а после простого года — интервалу от 29-го августа до 27-го сентября. При этом, никакие другие новолуния лунно-солнечного календаря на александрийский месяц тот не попадают. Из этого следует, что в I в. до н.э. пятое новолуние александрийского года (как простого, так и високосного) являлось первым после зимнего солнцестояния. По-видимому, это — не случайное совпадение. Скорее всего, александрийцы так сделали с умыслом, чтобы расписание новолуний в своём календаре было бы удобно синхронизировать с зимним солнцестоянием. Но тогда рассмотренный факт может служить дополнительным аргументом в пользу того, что самой ранней датой для первого новолуния после зимнего солнцестояния во время юлианской календарной реформы считалось именно 25-е декабря.

Ещё один любопытный факт можно найти в «Константинопольском списке консулов 395 г.» [1, с.333]. В этом историческом документе утверждается, что Иисус Христос родился 25-го декабря в «год консульства Августа и Сильвана» [1, с.335], соответствующий 2-му г. до н.э. [3, с.225]. Далее, в таблице 1 начальной датой для расчёта цикла с помощью алгоритма «−11 или +19» является 25-е декабря 59 г. до н.э. (декабрьская дата НЛСГ идёт перед январём года Г), а интервал между 59-м и 2-м гг. до н.э. составляет ровно три 19-летних периода: 59−2 = 3×19. Поэтому «Константинопольский список консулов 395 г.» относит рождество Христово на начало первого в цикле лунно-солнечного года (с номером А=1) одного из 19-летних периодов приведённого в таблице 1 цикла, из чего, по-видимому, следует, что этот цикл был известен составителям вышеупомянутого исторического документа.

Таким образом, реконструированный в настоящей главе лунно-солнечный календарь (первичное расписание новолуний в юлианском календаре) вполне мог быть составлен в I в. до н.э. по известным в то время календарным принципам. Однако исторических документов, содержащих свидетельства его практического использования, по-видимому, не существует. Осталось добавить, что к этому календарю, который условно назовём «цезаревским лунно-солнечным календарём» (или кратко «цезаревским календарём»), следует относиться как к гипотетическому календарю.

3. Альтернативное расписание новолуний в юлианском календаре для эпохи разрушения Иерусалимского храма

Иудейский календарь вплоть до IV в. н.э. основывался на реальных наблюдениях неомении — первого появления лунного серпа на вечернем небе. Обычно полагают, что специальная комиссия при иерусалимском синедрионе с помощью астрономических вычислений контролировала показания свидетелей, наблюдавших неомению. Вопрос же о переходе исключительно на вычисляемый лунно-солнечный календарь возник лишь после того, как в 70 г. н.э. Иерусалим был полностью разрушен войсками римского императора Веспасиана, а иудеи рассеялись по многим странам Европы и Азии. Вычисляемый иудейский календарь, официально действующий и сегодня, создавался в течение нескольких веков. В его основу положен тот же самый сирийский 19-летний цикл и то же самое вавилонское распределение эмболисмических годов в цикле, что получились при реконструкции цезаревского календаря. Поэтому правомерен вопрос: могли ли иудеи, например из Александрии, в тех случаях, когда запаздывало объявление синедриона о начале месяца, а вычисляемый календарь ещё не был официально введён, пользоваться цезаревским календарём, если, конечно, последний реально существовал?

В иудейском календаре, согласно Библии, религиозный год начинается с первого по счёту месяца авив — «месяца колосьев», в котором созревает ячмень. Но ячмень в окрестностях Иерусалима созревает весной, поэтому авив — месяц весенний. Позже этот месяц был переименован в месяц нисан, а началом гражданского года стал месяц тишри — седьмой месяц в религиозном году. Какие же месяцы в цезаревском календаре являются весенними? Поскольку лунно-солнечный год в этом календаре начинается в первое новолуние после зимнего солнцестояния, а промежуток времени между астрономическими моментами зимнего солнцестояния и весеннего равноденствия составляет чуть более трёх синодических месяцев, то под месяц нисан подходит либо третий, либо четвёртый лунный месяц.

Выбор конкретного месяца из указанных двух зависит от величины интервала между 25-м декабря и началом лунно-солнечного года. Очевидно, что при минимальных величинах этого интервала следует выбирать четвёртый месяц, а при максимальных — третий. Однако от величины этого же интервала зависит ещё и длина лунно-солнечного года: если интервал меньше 11 дней, то, согласно алгоритму «−11 или +19», год — эмболисмический. Этой корреляцией можно воспользоваться при промежуточных величинах рассматриваемого интервала, когда выбор нисана не очевиден и необходим дополнительный критерий. Действительно, самый простой способ выбора нисана в цезаревском календаре — это выбор четвёртого месяца в эмболисмических годах и третьего в простых (такие весенние месяцы в таблице 2 выделены курсивом). При этом как бы получается, что перенос нисана с третьего месяца на четвёртый обусловлен вставкой эмболисмического месяца именно перед этим нисаном, т.е. в конце религиозного года. Такой предложенный способ выбора нисана согласуется с исторически известным фактом, что эмболисмический месяц в древнем иудейском календаре вставлялся в конце религиозного года. Например, известно заявление председателя синедриона: «Поскольку голуби ещё малы и агнцы ещё очень молоды и к тому же время авива ещё не настало, то... мы признали за необходимое прибавить в этом году ещё тридцать дней» [1, с.246].

В вычисляемом иудейском календаре эмболисмический месяц веадар вставляется в конце религиозного года после 12-го месяца адар (перед нисаном). В эмболисмических годах адар имеет 30 дней, а веадар — 29; в простых же годах адар на один день короче, т.е. имеет 29 дней [2, с.120]. Если рассматривать не названия месяцев, а только их длину, то можно сказать, что 30-дневный эмболисмический месяц как бы вставляется не после 12-го месяца, а между 11-м и 12-м. Поскольку 11-й месяц — 30-дневный, то можно также сказать, что 30-дневный эмболисмический месяц как бы вставляется между 10-м и 11-м месяцами.

Таким образом, становится очевидной следующая переделка (модификация) цезаревского календаря в календарь «под иудейский»: 13-й месяц цезаревского календаря следует перенести в пределах эмболисмического года с последнего места на первое. При этом даты первых новолуний лунно-солнечных годов остаются прежними, а также сохраняется правило, что нечётные (уже по новой нумерации) месяцы — длинные, а чётные — короткие. Результат такой переделки показан в таблице 3. Если после этой (первой) переделки посмотреть на распределение длинных и коротких месяцев в году «от нисана до нисана» (нисан в таблице 3 выделен курсивом, а нумерация месяцев в году «от нисана до нисана» показана в последней строке), то получается следующая последовательность 30- и 29-дневных месяцев:

в которой «месяц в скобках» вставляется только в эмболисмических годах. Но именно такая же последовательность применяется и в так называемых «нормальных» лунно-солнечных годах вычисляемого иудейского календаря [2, с.120].

Таблица 3 Альтернативное расписание новолуний в юлианском календаре (с 13-м месяцем в начале лунно-солнечного года).
Обозначения: L — круг Луны сирийского цикла, точкой (•) обозначены эмболисмические годы; m — номер месяца в лунно-солнечном году (нечётный номер — 30-дневный месяц, чётный — 29-дневный), n — номер месяца при счёте от нисана, как в вычисляемом иудейском календаре (в первых трёх столбцах номера месяцев в эмболисмических годах указаны в скобках); курсивом обозначены новолуния весенних месяцев (нисана), жирным шрифтом — новолуния александрийского месяца тота, наклонным — новолуние нечётного, но 29-дневного месяца, т.е. месяца «скачка Луны»; звёздочкой (^_∗) обозначены новолуния месяца m=2, даты которых в високосные годы переносятся на один день назад.

В этой «нормальной» последовательности (назовём её альтернативной по отношению к созигеновской) используется уже обсуждавшаяся во второй главе формальная длина лунных месяцев, так как в таблице 3 юлианские високосные дни — 29-е февраля — вставляются «в скрытом виде». Эти дни попадают в основном на месяц m=2, но иногда и на месяц m=1. При этом реальная длина месяца по сравнению с формальной увеличивается на один день. В тех случаях, когда 29-е февраля попадает на месяц m=1, этот месяц получается длиной в 31 день, что определённо не подходит для иудейского календаря. Поэтому необходимо сделать ещё одну (вторую) переделку, а именно — ввести исключение: начинать месяц m=2 в високосных годах с кругами Луны L = 8, 11 и 19 на один день раньше (соответствующие новолуния отмечены в таблице 3 звёздочкой). В итоге, после второй переделки дополнительный день в високосных годах всегда вставляется в 29-дневном месяце m=2 и месяцев длиной в 31 день не получается. Заметим, что такие вставки, а также «скачок Луны» в месяце m=11 при L=16 (удаление лишнего дня) можно назвать корректировкой средней длины календарного года.

Подобная корректировка проводится и в вычисляемом иудейском календаре. Так, для некоторых годов этого календаря либо девятый от нисана 30-дневный месяц укорачивается на один день, либо восьмой от нисана 29-дневный месяц удлинняется. Однако в вычисляемом иудейском календаре, в отличие от таблицы 3, выбор года, длина которого корректируется либо вставкой добавочного дня, либо удалением лишнего, определяется на основе алгоритма, оперирующего с многозначными цифрами.

Сравнивая вычисляемый иудейский календарь (описание которого можно найти, например, в книге И.А. Климишина [1, с.245]) с календарём, приведённым в таблице 3, можно заключить, что они совпадают между собой по следующим четырём признакам. В обоих календарях используются: а) сирийский 19-летний цикл, б) вавилонское распределение в цикле эмболисмических годов, в) альтернативное чередование в «нормальных» годах (т.е. в годах без корректировки их длины) длинных и коротких месяцев и г) выбор девятого от нисана месяца для корректирующего удаления его 30-го дня. Однако в этих двух календарях различаются: а) математические алгоритмы, определяющие выбор года для корректировки его длины, и б) номера месяцев (при счёте от нисана) для корректирующей вставки в них 30-го дня.

Перечисленных совпадений вполне достаточно, чтобы предположить, что переделанный (модифицированный) цезаревский календарь (таблица 3) мог служить основой для создания вычисляемого иудейского календаря. Всё, что в ту эпоху осталось сделать — это разработать более точный алгоритм выбора года для корректировки его длины и перенести вставку корректирующего дня с месяца m=2 на месяц m=10. Необходимость таких изменений была обусловлена, по-видимому, недостаточной точностью расписания новолуний в таблице 3, так как это расписание, согласно Гиппарху, ошибается на одни сутки за каждые 304 года и в его одновременно високосных и эмболисмических годах четыре 30-дневных месяца идут подряд.

Анализируя таблицу 3, можно указать на дополнительный аргумент в пользу применения в цезаревском календаре именно созигеновского, а не альтернативного распределения длинных и коротких месяцев: в этой таблице последний месяц лунно-солнечного года с кругом Луны L=8 начинается 25-го декабря, т.е. в первое новолуние после зимнего солнцестояния, а первый месяц следующего года — только во второе новолуние, что определённо противоречит первому принципу цезаревского календаря, но, по-видимому, не имеет значения для иудейского.

Теперь посмотрим, как приведённое в таблице 3 расписание новолуний согласуется с астрономическими фазами Луны в том 19-летии, в котором Иерусалим был разрушен войсками императора Веспасиана. Этим 19-летием, если его начинать как и в таблицах 1–3 с года L=17, является интервал с 57-го по 75-й гг. н.э. Расчёт по методике, которая уже использовалась (во второй главе) для цезаревского календаря, показывает, что средний момент астрономического новолуния в 57–75 гг. н.э. приходился на 17 час 54 мин по иерусалимскому времени того дня, который предшествовал календарному новолунию таблицы 3, т.е. примерно за 6 часов до полуночи в начале первых суток лунного месяца. Этот результат хорошо согласуется с тем фактом, что сутки у иудеев начинаются накануне вечером при заходе Солнца (Библия, кн. Левит, гл.23:32). Поэтому сделанное выше предположение можно уточнить следующим образом: модифицированный цезаревский календарь (таблица 3), который условно назовём «альтернативным лунно-солнечным календарём» (или кратко «альтернативным календарём»), после разрушения Иерусалимского храма, т.е. начиная с 70-х гг. н.э., вполне мог быть прообразом действующего вычисляемого иудейского календаря.

При обсуждении привязки календарных новолуний к астрономическим необходимо обратить внимание на следующую особенность. Для простоты изложения рассмотрим сначала пример привязки к «идеальным» новолуниям, который иллюстрируется на Рис.1. На этом рисунке интервалы времени между «идеальными» новолуниями (штрихи на линии 1), заменяющими в данном примере астрономические, равны точно 29,5 суткам, а календарные лунные месяцы длиной в 30 и 29 дней чередуются попеременно (штрихи на линии 2). Оптимальной привязкой в этом примере будет такое расположение на оси времени начальных моментов «идеальных» и календарных месяцев, при котором «идеальное» новолуние совпадает в среднем с началом календарного месяца, т.е. при котором (см. Рис.1) 29,5-дневный интервал симметрично расположен внутри 30-дневного, а 29-дневный — внутри 29,5-дневного. Особенностью такой оптимальной привязки является то, что в этом случае «идеальное» новолуние приходится или на четверть суток позже начала 30-дневного календарного месяца, или на четверть суток раньше начала 29-дневного (см. разметку 3 на Рис.1). Расчёт показывает, что отмеченная особенность с хорошей точностью выполняется в среднем и для реальных новолуний.

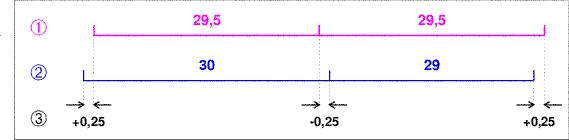Рис. 1 Иллюстрация оптимальной привязки лунного календаря к фазам Луны.
Обозначения: (1) — моменты времени «идеальных» новолуний с интервалом в 29,5 суток; (2) — начала календарных месяцев с попеременным чередованием длины в 30 и 29 дней; (3) — сдвижка (в сутках) момента времени «идеального» новолуния по отношению к началу календарного месяца.

Разделим все календарные лунные месяцы в таблице 3 на две группы: к первой группе отнесём 30-дневные месяцы, а ко второй — 29-дневные. В 57–75 гг. астрономические новолуния лунных месяцев как первой, так и второй группы приходились в среднем днём раньше соответствующих дат, приведённых в таблице 3. Однако в этих группах по отдельности средние моменты астрономических новолуний приходились на разное время: в первой группе — на 23 час 24 мин, а во второй — на 12 час 10 мин по иерусалимскому времени. Таким образом, особенностью уже реальной привязки лунно-солнечного календаря к фазам Луны является то, что по отношению к среднему моменту новолуния во всех месяцах цикла средний момент новолуния в 30-дневных месяцах цикла приходится примерно на 6 часов позже, а в 29-дневных — на 6 часов раньше. Можно также сказать: если средний момент новолуния во всех месяцах цикла приходится на закат, то средний момент новолуния в 30-дневных месяцах цикла — на полночь после этого заката, а в 29-дневных — на полдень до этого заката.

Месяц нисан в таблице 3 всегда имеет 30 дней, поэтому в 57–75 гг. средний за цикл момент астрономического новолуния в этом месяце приходился на полночь в начале первых суток, что хорошо согласуется с приведёнными в статье [7] пасхальными условиями привязки вычисляемого иудейского календаря к фазам Луны.

Заметим, что девятый месяц в таблице 3, выделенный жирным шрифтом, соответствует иудейскому месяцу тишри, в котором начинается гражданский новый год. Поэтому первое новолуние иудейского гражданского года, если его определять по таблице 3, и первое новолуние александрийского года соответствуют одному и тому же астрономическому новолунию.

Поэтому вполне возможно, что «предполагаемый прообраз вычисляемого иудейского календаря» связывался не только с юлианским календарём, но и с александрийским. Однако, «у историков, по-видимому, всё же имеется мало данных о том, что александрийский календарь получил широкое распространение. Так, писатель Цензорин в 238 г. подробно рассказывает о египетском календаре с его подвижным годом, но почему-то совершенно умалчивает об александрийском. Но уже столетием позже Феон Александрийский даёт исчерпывающие правила перехода от александрийских дат к египетским» [1, с.322].

Обратим внимание, что порядковый номер года в 19-летнем цикле (круг Луны) был определён пока только для лунно-солнечного года, начинающегося зимой — в первое новолуние после зимнего солнцестояния. А как перенести эту нумерацию на иудейские календарные годы, начинающиеся осенью (в гражданский новый год) и весной (в религиозный новый год)? Другими словами, как хронологически соотнести между собой годы, стоящие первыми в цикле, но относящиеся к разным стилям — к зимнему, осеннему и весеннему?

Будем исходить из того, что при любом стиле в цикле должно быть одно и то же распределение эмболисмических годов. Это условие будет выполняться, если годы, относящиеся к разным стилям, но содержащие внутри себя один и тот же эмболисмический месяц, будут иметь одно и то же значение для круга Луны. Учитывая сказанное, а также анализируя таблицу 3, где эмболисмический месяц помещён в начале «зимнего» года, можно сформулировать следующее правило: «осенний» год начинается раньше «зимнего», а «весенний» — раньше «осеннего». Например, согласно таблицам 1 и 3 начало первого после юлианской календарной реформы лунно-солнечного года с кругом Луны L=1 приходится на 21-е января 36 г. до н.э., но по осеннему и по весеннему стилям начало этого же года, т.е. с этим же кругом Луны L=1, приходится уже на 25-е сентября и на 1-е апреля 37 г. до н.э. соответственно.

Однако 1-го тишри 37 г. до н.э., если считать по осеннему стилю, начался не только иудейский (он же сирийский) 19-летний лунный цикл («малый круговорот»), но ещё и два других иудейских цикла — 7-летний цикл «субботнего года» и 28-летний солнечный цикл («большой круговорот»). У иудеев, согласно Библии, каждый седьмой год — это «суббота покоя земли» (кн. Левит, гл.25:4), т.е. так называемый «субботний год», в котором ограничиваются земледельческие работы. А 28-летний солнечный цикл — это период юлианского календаря, через который все его даты снова приходятся на те же дни недели. Действующий вычисляемый иудейский календарь практически не имеет периода повторяемости, поэтому можно предположить, что иудейский 28-летний цикл появился раньше него — в то время, когда создавался или уже был создан основанный на «расписании новолуний в юлианском календаре» прообраз вычисляемого иудейского календаря, и когда в иудейскую практику вводилась сдвижка даты нового года, если она выпадала на определённые дни недели — на воскресенье, среду и пятницу. Фактически это означало, что со сдвижками период повторяемости «расписания новолуний в юлианском календаре» увеличивался с 19-ти до 19×28 = 532-х лет. По определению все три цикла (лунный, солнечный и семилетний) начались 1-го тишри 1-го года иудейской эры от «сотворения мира», т.е. 7-го октября по ст.ст. 3761 г. до н.э. Именно поэтому число лет между 3761-м и 37-м гг. до н.э. в точности равно произведению длин этих трёх циклов: 3761−37 = 19×28×7. Любопытно, что в июле этого 37-го г. до н.э., в котором впервые после «сотворения мира» все три цикла снова сошлись вместе, библейский царь Ирод захватил Иерусалим и стал фактическим правителем Иудеи [3, с.281]. Заметим, что годы правления ветхозаветных царей отсчитывались от нисана (авива), т.е. по весеннему стилю.

В исторической литературе можно встретить четыре разных стиля летосчисления, определяемые выбором начала года — это так называемые январский, сентябрьский, мартовский и ультрамартовский годы [1, с.380]. Известно, что сентябрьский год начинается на четыре месяца раньше январского (с тем же обозначением), мартовский год — на шесть месяцев позже сентябрьского и ультрамартовский год — на шесть месяцев раньше сентябрьского. Сравнивая эти исторически известные стили с теми, которые были выше введены для таблицы 3, можно связать январский год с «зимним», сентябрьский — с «осенним», а ультрамартовский — с «весенним». Однако с чем же тогда связать исторически известный мартовский год?

Сохранив требование, чтобы годы, относящиеся к разным стилям, но содержащие внутри себя один и тот же эмболисмический месяц, имели бы одно и то же значение для круга Луны, проанализирум теперь таблицу 2, где, в отличие от таблицы 3, эмболисмический месяц помещён в конце «зимнего» года. В этом случае получается совсем другое правило: «весенний» год начинается позже «зимнего». Таким образом, если эмболисмическим месяцем «зимнего» года, считается месяц в конце этого года, то получается мартовский стиль, а если — в начале, то — ультрамартовский.

4. Расписание пасхальных полнолуний в юлианском календаре

При реконструкции цезаревского календаря, как уже отмечалось, получился исторически известный сирийский 19-летний цикл. Однако это значит только то, что эмболисмические годы цезаревского календаря и сирийского цикла совпали между собой. Что же касается совпадения в этих календарях юлианских дат новолуний, то здесь не всё так просто. Следует заметить, что использование сирийского цикла началось, по-видимому, в середине III в. н.э. [1, с.120], а к тому времени после юлианской календарной реформы уже прошло четыре цикла Калиппа или один цикл Гиппарха, т.е. 4×4×19 = 304 года. Действительно, первому году (L=1) сирийского цикла перед юлианской реформой соответствует 55 г. до н.э. (см. таблицу 1), а первому году этого же цикла в середине III в. н.э. — 250 г. Получается интервал в 304 года, из чего, согласно Гиппарху (см. главу 2), следует, что расписание новолуний в цезаревском календаре в середине III в. уже запаздывало по отношению к астрономическим новолуниям в среднем на одни сутки. А как соотносится это цезаревское расписание с датами новолуний сирийского цикла?

Для ответа на этот вопрос рассмотрим некоторые применявшиеся в средние века календарные характеристики. Сначала заметим, что кроме сирийского круга Луны для нумерации годов цикла широко использовалось так называемое золотое число александрийского цикла, которое на 3 больше круга Луны. В таблице 1 порядковый номер A, шаг алгоритма «−11 или +19», как раз удовлетворяет этому соотношению: A = L+3. Поэтому число A в таблице 1 — это не только номер года по порядку, но и золотое число. Однако сам цикл в таблице 1 не является александрийским, так как распределение его эмболисмических годов, пронумерованных с помощью числа A, не совпадает с вавилонским.

В хронологии было принято вычислять «возраст» Луны на некоторую фиксированную дату. Этот возраст (в днях) в системе включительного счёта, когда в счёт включался и день новолуния, был назван лунной эпактой. Обратимся теперь к таблице 1 и посмотрим, на какую же дату следует рассчитывать возраст «первой календарной Луны» в лунно-солнечном году. Очевидно, что этой датой должно быть самое позднее начало лунно-солнечного года, которое в таблице 1 выпадает на 23-е января. Если выбрать другую дату, то соответствующий возраст уже не будет относиться к «первой календарной Луне» как минимум в одном из двух лунно-солнечных годов с номерами A=1 и A=12. Рассчитанный на 23-е января по включительному счёту возраст Луны — лунная эпакта — приведён для каждого года 19-летнего цикла в столбце EL таблицы 1. Поскольку суммарная длина января и февраля (31+28 = 59 дней) равна суммарной длине двух календарных лунных месяцев (30+29 = 59 дней), то возраст Луны на 23-е января и на 23-е марта будет один и тот же. Поэтому лунную эпакту в таблице 1 можно также назвать и возрастом Луны по включительному счёту на 23-е марта.

Сравним лунные эпакты, приведённые в таблице 1 для цезаревского календаря, с теми лунными эпактами, которые в средние века использовались как для расчётов дат Пасхи, так и для датировки документов. Средневековые лунные эпакты можно найти в книге И.А. Климишина [1, с.119, 140]. Сравнение показывает, что все лунные эпакты в таблице 1 в точности совпадают со средневековыми. Однако последние определяются не как возраст Луны на 23-е марта, а как возраст на 22-е марта. Таким образом, даты новолуний, определяемые по средневековым лунным эпактам, приходятся на день раньше, чем в цезаревском календаре.

Другой календарной характеристикой в средние века были лунные регуляры, которые позволяли рассчитывать возраст (фазу) Луны на первое число любого юлианского месяца в любом году 19-летнего цикла по известным фазам на первые числа месяцев в первом году цикла. Лунные регуляры для цезаревского календаря, т.е. возраст Луны по включительному счёту на первое число каждого юлианского месяца в году с золотым числом A=1 (или с кругом Луны L=17) 19-летнего цикла, приведены в таблице 4. Сравнение этих регуляров со средневековыми лунными регулярами, которые также можно найти в книге И.А. Климишина [1, с.144], показывает, что средневековые регуляры все без исключения на единицу больше. Таким образом, как и в случае с лунными эпактами, даты новолуний, определяемые по средневековым лунным регулярам, приходятся на день раньше, чем в цезаревском календаре.

Таблица 4 Лунные регуляры — возраст Луны по включительному счёту на первое число каждого юлианского месяца в первом (A=1 или L=17) году цикла цезаревского календаря.

Следующей важной календарной характеристикой являются юлианские даты пасхальных полнолуний, которые определяются как 14-й день весеннего (пасхального) лунного месяца. Как уже обсуждалось в третьей главе, весенними (пасхальными) месяцами в цезаревском календаре (таблица 2) являются третьи лунные месяцы в простых годах цикла и четвёртые в эмболисмических. Юлианские даты пасхальных полнолуний в цезаревском календаре приведены в столбце ППЦК таблицы 5 в зависимости от порядкового номера A (шага алгоритма «−11 или +19») и от сирийского круга Луны L. В этой же таблице в столбце ППСЦ приведены для сравнения юлианские даты пасхальных полнолуний сирийского цикла, взятые из статьи В.В. Болотова [8, с.109]. Как видно, все без исключения пасхальные полнолуния сирийского цикла приходятся на один день раньше, чем в цезаревском календаре.

Таблица 5 Юлианские даты пасхальных полнолуний в разных календарях.
Обозначения: A — номер по порядку; L, N и G — номера годов в сирийском цикле (СЦ), в цикле Анатолия Лаодикийского (АЛ) и в александрийском цикле (АЦ); ППЦК, ППСЦ, ППАЛ и ППАЦ — даты пасхальных полнолуний в цезаревском календаре, а также в циклах СЦ, АЛ и АЦ. Точкой (•) во всех циклах обозначены эмболисмические годы, жирным шрифтом — пасхальное полнолуние первого года цикла, курсивом — самое раннее пасхальное полнолуние в цикле.

Подводя итоги сравнения цезаревского календаря с исторически известными календарными характеристиками — с лунными эпактами, с лунными регулярами и с юлианскими датами пасхальных полнолуний, можно сделать следующий вывод: расписание новолуний сирийского цикла могло быть получено в III в. из цезаревского календаря с помощью поправки Гиппарха, т.е. с помощью сдвижки всех дат новолуний на одни сутки назад. Конечно, этот вывод имеет смысл, если исходный цезаревский лунно-солнечный календарь действительно был реальным календарём.

Как видно из таблицы 5 самой ранней датой пасхального полнолуния в цезаревском календаре является 19-е марта. Поскольку речь идёт о 14-м дне именно весеннего лунного месяца, то дату 19-го марта — границу пасхального полнолуния — можно рассматривать как критерий весеннего месяца: лунный месяц является весенним, если его 14-й день наступает 19-го марта или позже. Однако, из-за поправки Гиппарха эта граница в сирийском цикле (см. таблицу 5) переместилась на 18-е марта, т.е. получилось, что как бы поменялся критерий весеннего месяца. Но по своему определению юлианский календарь привязан именно к движению Солнца и (вплоть до григорианской реформы) никаких поправок в нём не предполагалось. Поэтому далеко не все христианские пасхалисты могли быть удовлетворены сменой в солнечном календаре критерия весеннего месяца.

В пользу этого утверждения говорит отрывок «Из Анатолиевых правил о Пасхе», приведённый в «Церковной истории» Евсевия Кесарийского: «В первом году новолуние первого месяца, являющееся началом девятнадцатилетнего периода, приходится для египтян на 26-е число месяца фаменота, для македонян — на 22-е число месяца дистра, или, как сказали бы римляне, на 11-е число до апрельских календ. 26-го числа упомянутого месяца фаменота Солнце не только вступает в первое созвездие, но идёт по нему уже четвёртый день. Это созвездие (Овен) обычно называют первым из двенадцати, равноденственным, началом года...» [9, с.331]. В этом же отрывке также утверждается, что иудейские авторитеты, «...разрешая вопросы, касающиеся Исхода, говорят, что равным образом все должны приносить пасхальные жертвы после весеннего равноденствия, в середине первого месяца, т.е. когда Солнце проходит первую часть эклиптики, или, как некоторые называют, зодиака» [9, с.331]. С помощью синхронистических таблиц [1, с.226, 290] получаем, что 26-е число месяца фаменота и 11-е число до апрельских календ соответствуют 22-му марта по ст.ст. Следовательно, в цитируемом отрывке говорится, что в первое созвездие зодиака Солнце вступает 19-го марта (1-й, 2-й, 3-й и 4-й дни — это 19-е, 20-е, 21-е и 22-е марта). А так как, согласно Библии, пасхальные жертвы приносятся 14-го числа, то из цитированного отрывка также следует, что 14-е число весеннего месяца — пасхальное полнолуние — должно приходиться на 19-е марта или позже. Таким образом, у Анатолия Лаодикийского границей пасхального полнолуния является 19-е марта. Но, может быть, он говорит о цезаревском календаре?

Анатолиев цикл начинается 22-го марта, поэтому в этом цикле первое пасхальное полнолуние приходится на 22+13 = 35 марта или 4 апреля. Но в цезаревском календаре ни одно из пасхальных полнолуний не попадает на эту дату (см. столбец ППЦК в таблице 5). Тогда о каком же цикле идёт речь? Об этом цикле известно лишь то, что в нём самое раннее пасхальное полнолуние приходится на 19-е марта, а первое в цикле — на 4-е апреля. Поэтому можно только предположить как был составлен этот цикл: Анатолий Лаодикийский, по-видимому, за основу своего цикла взял сирийский цикл, но решил оставить в нём ту же границу пасхального полнолуния, что была в цезаревском календаре — 19-е марта. Для этого, в принципе, вполне было бы достаточно в году с кругом Луны L=16 перенести дату пасхального полнолуния на один лунный месяц вперёд — с 18-го марта на 17-е апреля. Однако, если этим только и ограничиться, то нарушится правило: «пасхальный месяц — это третий месяц в простом году, но четвёртый в эмболисмическом». Чтобы сохранить это правило, можно поступить следующим образом: первый месяц эмболисмического года с кругом Луны L=17 объявить последним месяцем предшествующего простого года с кругом Луны L=16 (см. переход от исходного пункта a к пункту b на Рис.2). Тогда год L=16 становится эмболисмическим и его пасхальное полнолуние по вышеприведённому правилу переносится на один месяц вперёд. При этом год L=17 становится простым и с несозигеновской последовательностью длинных и коротких месяцев. Поэтому на следующем шаге уже в простом году L=17 чередование длины месяцев меняется на обратную (на Рис.2 — это переход от пункта b к пункту c).

Рис. 2 Иллюстрация изменения структуры лунно-солнечного календаря при переносе пасхального полнолуния на один месяц вперёд.
Обозначения: Эмболисмический год обведён сплошной рамкой; простой год — пунктирной; заштрихованные символы — 30-дневные месяцы, пустые — 29-дневные; квадратные символы — пасхальные месяцы, круглые — все остальные; в пункте a) показана начальная структура простого (с кругом Луны L=16) и эмболисмического (с кругом Луны L=17) годов; в пункте b) первый месяц года L=17 объявляется последним месяцем года L=16, так что год L=16 становится эмболисмическим, а год L=17 — простым; в пункте c) в году L=17 последовательность длинных и коротких месяцев меняется на обратную. Поскольку год L=16 стал эмболисмическим, то его пасхальный месяц — четвёртый (вместо третьего).

Результат реконструкции юлианских дат пасхальных полнолуний по предложенной схеме показан в столбце ППАЛ таблицы 5. Эти даты образуют цикл, в котором по сравнению с сирийским изменилась не только дата самого раннего пасхального полнолуния, но и последовательность эмболисмических годов. Если теперь «по-вавилонски» пронумеровать годы реконструированного цикла, т.е. так, чтобы эмболисмическими были 3-й, 6-й, 8-й, 11-й, 14-й, 17-й и 19-й годы (см. столбец N в таблице 5), то получится, что цикл начинается в год c кругом Луны L=9. Далее, из столбца ППАЛ таблицы 5 видно, что первое пасхальное полнолуние цикла приходится на 4-е апреля, а самое раннее — на 19-е марта (в году с L=5 или N=16). Поэтому реконструированный цикл в точности согласуется с отрывком «Из Анатолиевых правил о Пасхе» [9, с.331] и его вполне можно назвать циклом Анатолия Лаодикийского. По мнению большинства исследователей [10, с.170] этот цикл начался в 277 г. н.э.

В эпоху создания анатолиева цикла граница его пасхального полнолуния приходилась раньше даты весеннего равноденствия, которое, если началом суток считать полночь по александрийскому времени, выпадало в 192–359 гг. на 20–21 марта. Поэтому не исключено, что Анатолий Лаодикийский пользовался какой-то древней системой деления эклиптики, в которой привязанное к неподвижным звёздам начало первого зодиакального созвездия (Овна) находилось западнее точки весеннего равноденствия на некоторый угол d. Например, анализ «египетских планетных таблиц» [11, с.326], содержащих «даты вхождений планет в знаки зодиака», показывает, что во второй декаде царствования императора Августа (т.е. в 20–11 гг. до н.э.) египетские математики пользовались сидерическим (определяемым относительно неподвижных звёзд) делением эклиптики с углом d равным в среднем 4°. Учитывая этот факт, а также то, что в указанные годы весеннее равноденствие в среднем приходилось на 23-е марта (см. Рис.3, на котором приведены расчёты по формулам Ж. Меёса [6]), можно сделать вывод, что в Египте в конце I в. до н.э. Солнце входило в знак Овна на четыре дня раньше весеннего равноденствия, т.е. 19-го марта. Именно эта дата получилась для границы пасхального полнолуния в цезаревском календаре. Возможно, что такое совпадение не является случайным.

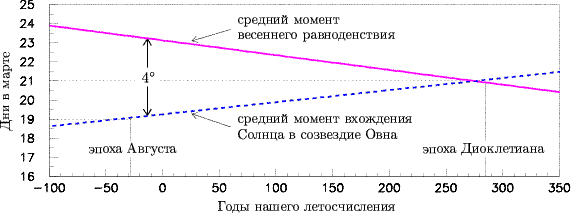Рис. 3 Изменение с годами в юлианском календаре средних моментов весеннего равноденствия и вхождения Солнца в созвездие Овна по египетскому делению зодиака.
Обозначения: Сплошная и пунктирная линии — средние за каждые четыре года моменты весеннего равноденствия и вхождения Солнца в созвездие Овна (с началом суток от полуночи по александрийскому времени). Показан интервал в 4° между началом зодиака и точкой весеннего равноденствия для эпохи 20–11 гг. до н.э., как это следует из анализа «египетских планетных таблиц» [11, с.326].

В день равноденствия, когда центр Солнца пересекает небесный экватор, принято считать, что «день равен ночи». Однако это утверждение относится к так называемой астрономической продолжительности светового дня, которая как бы в отсутствие земной атмосферы определяется как интервал времени между утренним и вечерним моментами пересечения центром Солнца линии горизонта. Если же определять видимую продолжительность светового дня, т.е. интервал времени между появлением первых и исчезновением последних лучей Солнца, то необходимо учитывать как угловой диаметр Солнца, так и астрономическую рефракцию — преломление света в земной атмосфере, из-за которой светило остаётся видимым даже тогда, когда оно находится под горизонтом «на глубине» несколько превышающей угловой диаметр Солнца. Расчёт показывает, что на широте Александрии в дни, близкие к весеннему равноденствию, продолжительность видимого светового дня ежедневно увеличивается примерно на 1,9 минуты, а непосредственно в сам день весеннего равноденствия видимый световой день длиннее астрономического примерно на 7,7 минуты [1, с.27]. Получается, что в Александрии примерно за 7,7:1,9 = 4 дня до прохождения Солнцем точки весеннего равноденствия день от первых до последних лучей Солнца равен ночи от последних до первых лучей Солнца. Не этим ли объясняется выбор начала зодиака египетскими математиками в конце I в. до н.э.?

Можно также предположить, что Анатолий взял свою границу пасхального полнолуния из цезаревского календаря, в котором она определялась автоматически из правила: «пасхальный месяц — это третий месяц в простом году, но четвёртый в эмболисмическом». Эта граница в конце I в. до н.э., хотя и была близка к точной дате весеннего равноденствия, но всё же не совпадала с ней, так как цезаревский календарь, согласно сформулированным в настоящей статье принципам, был привязан именно к зимнему солнцестоянию, а не к весеннему равноденствию. Граница же пасхального полнолуния сирийского цикла, если этот цикл действительно был получен из цезаревского календаря с помощью поправки Гиппарха, могла не подходить для Анатолия, так как ему, возможно, было известно, что Солнце, проходя вблизи некоторых звёзд 19-го марта в эпоху Августа, не будет проходить вблизи этих же звёзд раньше 19-го марта в его эпоху (что не противоречит астрономическим данным той эпохи: по Гиппарху время полного оборота Солнца на небосводе относительно неподвижных звёзд примерно на 10 минут превышает юлианский год длиной в 365,25 дней [12, с.407]).

Однако ко времени проведения Никейского собора (325 г.) александрийскими пасхалистами настойчиво был выдвинут принцип, что Пасха должна совершаться непременно после весеннего равноденствия, определяемого по астрономическим наблюдениям современной им эпохи. Самый простой способ удовлетворить этому требованию — это перенести дату самого раннего пасхального полнолуния в анатолиевом цикле на один месяц вперёд. Сделать это можно с помощью всё того же способа, который уже описан при реконструкции анатолиева цикла из сирийского: пасхальное полнолуние в анатолиевом цикле в году N=16 переносится с 19-го марта на 18-е апреля; этот год становится эмболисмическим, а следующий за ним — простым, в котором затем восстанавливается созигеновская последовательность длинных и коротких месяцев (см. Рис.2). Получившийся цикл, который приведён в таблице 5 вместе с вавилонской нумерацией своих годов (столбцы ППАЦ и G), является исторически известным александрийским пасхальным циклом [8, с.109], применяющимся в настоящее время в православной пасхалии. Как видно из указанной таблицы, в александрийском цикле самое раннее пасхальное полнолуние приходится на 21-е марта, т.е. начиная с III в. — не раньше весеннего равноденствия.

Из астрономических данных известно, что момент прохождения Солнцем точки весеннего равноденствия смещается в юлианском календаре на один день назад примерно за 128 лет, а момент прохождения им неподвижной звезды — на один день вперёд примерно за 157 лет. Поэтому, если Солнце в конце I в. до н.э. проходило некоторую звезду 19-го марта, то в конце III в. н.э. эту же звезду оно проходило уже 21-го марта. Такая зависимость иллюстрируется на Рис.3, на котором для сравнения отмечены ещё и даты прихода к власти в Египте римских императоров Августа (1 августа 30 г. до н.э.) и Диоклетиана (29 августа 284 г. н.э.). Таким образом, границы пасхальных полнолуний в цезаревском календаре в эпоху Августа и в александрийском цикле в эпоху Диоклетиана соответствуют одному и тому же положению Солнца на эклиптике относительно неподвижных звёзд, которое, по-видимому, в обе эпохи было у египтян началом зодиака. Возможно, что александрийские астрономы в конце I в. до н.э. выбрали за начало знака Овна именно ту точку, в которой Солнце в те годы находилось 19-го марта — в самую раннюю юлианскую дату, на которую выпадал 14-й день весеннего месяца в цезаревском лунно-солнечном календаре. Интересно отметить любопытный факт — летосчисление по эре Диоклетиана началось вскоре после того, как точка весеннего равноденствия совпала с египетским началом зодиака (см. Рис.3).

Обратим ещё внимание и на следующие факты. Вавилонская нумерация годов александрийского цикла — золотые числа — совпадает с нумерацией, в которой используются порядковые номера, получившиеся при реконструкции цезаревского календаря с помощью алгоритма «−11 или +19», т.е. G = A (см. таблицу 5). Далее, при реконструкции как анатолиева цикла из сирийского, так и александрийского цикла из анатолиева начало одного из лунно-солнечных годов переносится на один месяц вперёд (см. Рис.2). В результате этих переносов самая поздняя юлианская дата для первого календарного новолуния лунно-солнечного года в александрийском цикле приходится не на 22-е января, как в сирийском цикле, а на 25-е января. Поскольку исторически известные лунные эпакты определяются как возраст Луны по включительному счёту всё-таки на 22-е января (или на 22-е марта, что эквивалентно), то получается, что в сирийском цикле лунная эпакта — это возраст именно «первой календарной Луны», а в александрийском цикле — не обязательно «первой». По-видимому, это говорит о том, что лунная эпакта, определяемая как возраст Луны на 22-е января, сначала была введена именно для сирийского цикла, иначе какой же был у неё смысл, если в александрийском цикле дата «22-е января» никак не выделена?

Как уже отмечалось во второй главе, в цезаревском календаре средний момент астрономического новолуния изначально приходился примерно на 6 часов утра по александрийскому времени в начале первых суток лунного месяца. В 19-летии, в котором была проведена юлианская календарная реформа, год с кругом Луны L=1 приходился в цезаревском календаре на 55 г. до н.э., а через цикл Гиппарха — на 250 г. н.э. За эти 304 года «среднее астрономическое новолуние» стало опережать цезаревский календарь на одни сутки, но в сирийском цикле оно было «возвращено на изначальное место». Однако к 326 г., к первому после Никейского собора году с кругом Луны L=1, средний момент астрономического новолуния уже и в сирийском цикле сместился назад на четверть суток, потому что интервал времени между 250 и 326 гг. составлет 76 лет — четвёрть цикла Гиппарха. Поэтому в эпоху Никейского собора средний момент астрономического новолуния в сирийском цикле приходился примерно на полночь по александрийскому времени в начале первых суток лунного месяца. Этот момент является усреднённым по всем месяцам цикла, но поскольку пасхальные месяцы в цезаревском календаре, а значит и в сирийском цикле, имеют разные длины (30 или 29 дней), то можно утверждать, что и в пасхальных месяцах сирийского цикла средний момент астрономического новолуния в эпоху Никейского собора приходился примерно на полночь по александрийскому времени в начале первых суток (см. главу 3).

Календарные новолуния сирийского и александрийского циклов в 223-х месяцах совпадают между собой, а в 12-ти различаются на один день. Это различие связано с тем, что при переделке сирийского цикла в александрийский, как описано выше, два эмболисмических года становятся простыми, а их последовательности длинных и коротких месяцев меняются на обратные (см. Рис.2). Так как календарные новолуния обоих циклов в основном совпадают, то средний момент астрономического новолуния в александрийском цикле в эпоху Никейского собора также приходился примерно на полночь в начале первых суток лунного месяца. Расчёт подтверждает сказанное: в 323–341 гг. усреднённый по всем 235-ти месяцам александрийского цикла момент новолуния приходился на 23 час 47 мин по александрийскому времени в ночь на первые сутки лунного месяца. Этот расчёт интересно сравнить со свидетельством римского писателя Цензорина, жившего в III в. н.э., который утверждает, что у римлян сутки начинались от полуночи [1, с.281].

Конечно, оптимальной привязкой лунно-солнечного календаря к фазам Луны является такая привязка, при которой средний момент астрономического новолуния приходится на начало первых суток лунного месяца. При этом заметим, что христианские циклы создавались главным образом для вычисления дат Пасхи, имеющей, как известно, иудейское происхождение, и что в иудейском календаре сутки начинаются накануне вечером при заходе Солнца. Нет ли противоречия в том, что средний момент астрономического новолуния в александрийском цикле в эпоху Никейского собора приходился именно на полночь (начало суток у римлян), а не на заход Солнца накануне вечером (начало суток у иудеев)? Противоречия нет, если к указанной эпохе в иудейском календаре уже сложилась традиция устанавливать длину пасхальных месяцев только в 30 дней (как в действующем вычисляемом календаре), а христианские пасхалисты при составлении своих циклов принимали во внимание привязку к фазам Луны именно пасхальных месяцев цикла или месяцев той же длины, что у пасхальных. Действительно, в третьей главе уже обсуждалось (см. Рис.1), что если усреднённый по всем месяцам цикла момент астрономического новолуния приходится на закат, то усреднённый только по 30-дневным месяцам — на 6 часов позже, т.е. на полночь. Поэтому, если в иудейском календаре все месяцы его 19-летнего цикла оптимально привязаны к фазам Луны, а пасхальные месяцы всегда имеют длину в 30 дней, то момент астрономического новолуния, усреднённый в этом календаре только по пасхальным или только по 30-дневным месяцам цикла, также приходится на полночь (начало суток у римлян), как и в александрийском цикле в эпоху Никейского собора.

Расписания новолуний в юлианском календаре для сирийского, анатолиева и александрийского циклов можно получить из таблицы 5, в которой для этих циклов приведены юлианские даты пасхальных полнолуний и указаны эмболисмические годы, и из правила, что «пасхальный месяц — это третий месяц в простом году, но четвёртый в эмболисмическом». Сначала для каждого лунно-солнечного года цикла вычисляется дата его первого новолуния, которая в простом году приходится раньше даты пасхального полнолуния на 30+29+13 = 72 дня, а в эмболисмическом — на 30+29+30+13 = 102 дня. Затем по созигеновскому принципу распределяются лунные месяцы: нечётный месяц — 30-дневный, чётный — 29-дневный. «Скачок Луны» помещается в последний 30-дневный месяц года с номером A=19. Реконструированное таким образом расписание новолуний в юлианском календаре для александрийского цикла, называемое также «Вечным лунно-солнечным церковным календарём», приведено в статье А.М. Эфросмана [4, с.356–357]. Аналогичным же образом можно составить расписания новолуний в юлианском календаре и для других (см. следующую главу) распределений в лунно-солнечном году длинных и коротких месяцев.

Итак, три исторически известных пасхальных цикла могут быть последовательно получены из гипотетического цезаревского календаря:

5. Средневековый лунно-солнечный церковный календарь и христианские эры от «сотворения мира»

Как уже отмечалось, лунные эпакты и лунные регуляры в цезаревском календаре строго на единицу меньше, чем в средневековом лунно-солнечном календаре. Поэтому, казалось бы, если в цезаревском календаре сдвинуть даты всех новолуний на один день назад (назовём это лунной поправкой), а затем даты двух самых ранних пасхальных полнолуний перенести по описанной в предыдущей главе методике на один месяц вперёд (назовём это солнечной поправкой), то должен получиться средневековый календарь. Однако это не так. Как показывает анализ дошедших до нас вариантов средневекового календаря, приведённых в книгах М.Н. Лалоша [13, с.94–95], Ф.К. Гинцеля [14, с.136] и И.А. Климишина [1, с.440], в этих вариантах: во-первых, даты пасхальных полнолуний всегда совпадают с соответствующими датами александрийского цикла, и, во-вторых, длины пасхальных месяцев всегда составляют 29 дней. Кроме того, из этого анализа следует, что приведённые варианты средневекового календаря дополнены новым принципом: в эмболисмических годах длинные и короткие месяцы распределены так же, как и в цезаревском календаре, но в простых годах — в обратном порядке. Однако этот принцип имеет некоторые исключения, несколько различающиеся для разных вариантов средневекового календаря.

В таблице 6 приведён лунно-солнечный календарь, который получился из цезаревского календаря с помощью описанных выше лунной и солнечной поправок, а также с помощью замены в простых годах цикла созигеновской последовательности длинных и коротких месяцев (30—29) на обратную (29—30). При составлении таблицы 6 порядок месяцев в эмболисмических годах не был изменён, но эти месяцы перенумерованы так, что 13-й месяц формально оказался в начале года. Это сделано для удобства: при такой перенумерации вставной (т.е. 13-й) и все чётные месяцы имеют по 30 дней, а все нечётные — по 29. Даты новолуний, приведённые в таблице 6, совпадают с соответствующими датами средневекового календаря из книги М.Н. Лалоша [13, с.94–95] во всех случаях за следующим исключением: новолуния, отмеченные жирным шрифтом, приходятся на день позже соответствующих новолуний из книги Лалоша, а новолуния, отмеченные наклонным шрифтом, — на день раньше. Так как исключений немного, то таблицу 6 можно назвать основой средневекового лунно-солнечного календаря. Но почему средневековые пасхалисты, к которым в первую очередь относятся римский монах VI в. Дионисий Малый и церковный историк VIII в. Беда Достопочтенный, изменили последовательность длинных и коротких месяцев в простых годах цикла? Чтобы ответить на этот вопрос рассмотрим дополнительные исторические факты.

Таблица 6 Основа средневекового расписания новолуний в юлианском календаре.
Обозначения: G — золотое число, точкой (•) обозначены эмболисмические годы; m — номер месяца в лунно-солнечном году (13-й и чётные номера — 30-дневные месяцы, нечётные номера — 29-дневные); курсив — новолуния пасхальных месяцев. Даты новолуний, приведённые в настоящей таблице, совпадают с соответствующими датами средневекового календаря из книги М.Н. Лалоша [13, с.94–95] во всех случаях за следующим исключением: новолуния, отмеченные жирным шрифтом, приходятся на день позже соответствующих новолуний из книги Лалоша, а новолуния, отмеченные наклонным шрифтом, — на день раньше.

Александрийская пасхалия (таблица дат пасхальных воскресений — дат празднования Пасхи) повторяется через каждые 532 года. Этот период, называемый великим индиктионом, получается при перемножении лунного периода в 19 лет и солнечного в 28 лет (19×28 = 532), так как через каждые 19 лет все фазы Луны приходятся на те же даты юлианского календаря, а через каждые 28 лет все даты юлианского календаря приходятся на те же дни недели. Однако 532 года — это большой период. Из практических соображений александрийские епископы составляли пасхалии на 19×5 = 95 лет, на так называемый малый пасхальный круг. При составлении новой пасхалии на следующие 95 лет в старую пасхалию просто вносились поправки, причём исправлять приходилось примерно одну четверть дат, а остальные даты в старой и новой пасхалиях совпадали [1, с.331].

Александрийские и римские даты празднования Пасхи по ряду причин [1, с.292] не всегда совпадали между собой вплоть до начала VI в. В первые десятилетия после Никейского собора (325 г.) александрийцы, пытаясь найти согласие с римлянами, несколько раз назначали компромисную дату Пасхи, отличающуюся от александрийской пасхалии. Однако после издания александрийским патриархом Феофилом в 380 г. «столетнего канона» александрийская пасхалия для александрийцев стала обязательной [10, с.223]. Ещё задолго до окончания действия этого канона александрийский патриарх Кирилл составил новую пасхалию на 95 лет, с 437-го по 531-й гг. Продлить же эту пасхалию на очередные 95 лет было поручено в 525 г. настоятелю монастыря св. Анастасия в Риме Дионисию Малому [4, с.351].

В то время, когда вводилась пасхалия Феофила Александрийского, летосчисление в Египте велось по эре Диоклетиана и 380-й г. н.э. считался 96-м г. эры Диоклетиана. Поэтому напрашивается очевидное предположение, что Феофил Александрийский всего лишь продлил уже имевшуюся пасхалию, составленную на 95 лет от начала эры Диоклетиана, с 285-го по 379-й гг. н.э. Это предположение усиливается тем, что в пасхалии Феофила «годы не были отнесены к какой-либо эре, а обозначались порядковыми номерами» [4, с.352]. Из чего, возможно, следует, что новая пасхалия была получена путём исправления старой, причём годы эры Диоклетиана (с 1-го по 95-й) не были исправлены, превратившись, таким образом, в порядковые номера.

Особенностью эры Диоклетиана является то, что она началась 29 августа 284 г., а днём раньше этой даты было астрономическое новолуние. Стоит также добавить, что к началу этой эры, как показано на Рис.3, точка весеннего равноденствия, которая в следствие прецессии движется по эклиптике относительно неподвижных звёзд, совпала с началом египетского сидерического зодиака эпохи императора Августа. Однако есть ещё одна особенность.

Но сначала заметим, что «расписание новолуний в юлианском календаре» с александрийскими пасхальными полнолуниями, которое далее будем называть Вечным календарём, может быть составлено (как описано в главе 4) с любым из следующих трёх распределений в году 30- и 29-дневных (длинных и коротких) лунных месяцев:

где в скобках показан 13-й месяц в эмболисмическом году. Созигеновское распределение используется в цезаревском календаре, а также в «Вечном лунно-солнечном церковном календаре» [4, с.356–357], альтернативное — в предполагаемом прообразе вычисляемого иудейского календаря (см. главу 3), и средневековое — в календаре, приведённом в таблице 6.

Итак, ещё одной особенностью эры Диоклетиана является то, что в 19-летие непосредственно перед началом этой эры (т.е. в 266–284 гг. н.э.) средний момент астрономического новолуния в Вечном календаре с александрийскими пасхальными полнолуниями, но с альтернативным распределением длинных и коротких месяцев пришёлся на полночь в начале первых суток лунного месяца, точнее на 0 час 5 мин по александрийскому времени (расчёт сделан по той же методике, что и во второй главе). Линия 2 на Рис.4 показывает, как этот момент изменяется с годами.

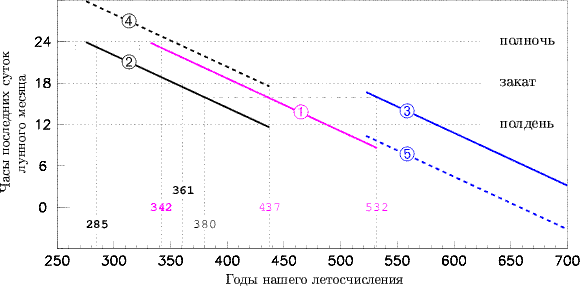Рис. 4 Изменение с годами среднего момента астрономического новолуния относительно начала лунного месяца в «Вечном лунно-солнечном церковном календаре».
Обозначения: Линии (1), (2) и (3) — усреднённые по всем месяцам цикла моменты астрономических новолуний в «Вечных календарях» с созигеновским, альтернативным и средневековым распределениями длинных и коротких месяцев; линия (4) — то же, что и линия (2), но только для 30-дневных месяцев цикла; линия (5) — то же, что и линия (3), но только для 29-дневных месяцев цикла. Средние моменты астрономических новолуний определены по александрийскому времени для каждого 19-летнего интервала, а затем аппроксимированы прямой линией.

Кирилл Александрийский составил свою пасхалию начиная с 437-го г. н.э. Отняв от этого года 95 лет, получаем 342-й г. Но последнее 19-летие перед 342-м г., т.е. 19-летие с 323-го по 341-й гг., имеет свои особенности. В этом 19-летии, во-первых, состоялся Никейский собор и, во-вторых, средний момент астрономического новолуния в Вечном календаре с александрийскими пасхальными полнолуниями, но с созигеновским распределением длинных и коротких месяцев пришёлся, как уже обсуждалось в главе 4, на полночь в начале первых суток лунного месяца, точнее на 23 час 47 мин по александрийскому времени. Линия 1 на Рис.4 показывает, как этот момент изменяется с годами.

Таким образом, получается, что пасхалия Феофила Александрийского была составлена на второе 95-летие эры Диоклетиана, а пасхалия Кирилла Александрийского — на второе 95-летие другой эры, которую назовём эрой Никейского собора. Далее, выбор александрийцами именно этих эр для своих пасхальных расчётов был обусловлен, конечно, рядом исторических обстоятельств. Однако, всё же, главной причиной этого выбора был, по-видимому, тот факт, что средний момент астрономического новолуния в Вечном календаре приходился практически на полночь по александрийскому времени в начале первых суток лунного месяца, если в этом календаре для эпохи Диоклетиана использовалось альтернативное распределение длинных и коротких месяцев, а для эпохи Никейского собора — созигеновское. Из этого, скорее всего, следует, что в основе пасхалии Феофила лежал Вечный календарь с альтернативным распределением длинных и коротких месяцев, а в основе пасхалии Кирилла — с созигеновским.

Поэтому вполне можно согласиться с A.M. Эфросманом, который называет последовательность длинных и коротких месяцев в «Вечном лунно-солнечном церковном календаре», приведённом в его статье, именно как «распределение "по Созигену и Кириллу Александрийскому"». Однако сам календарь он приводит как «"Вечный лунно-солнечный календарь Дионисия Малого" в переработанном для целей данной работы виде», причём уточнение «в переработанном виде» почему-то отсутствует в заголовке соответствующей таблицы, что даёт повод для критики [4, с.355–357].

Следует ещё отметить, что в литературе (см., например, [4, с.354]), говоря о «начале» Вечного календаря, обычно упрощаются детали его привязки к лунным фазам: считается, что Вечный календарь был приурочен либо к эре Диоклетиана, так как 29-го августа 284 г. (в первый день эры Диоклетиана) была неомения, либо к году Никейского собора, так как 1-го марта 325 г. (в первый по мартовскому стилю день года Никейского собора) было астрономическое новолуние.

Теперь становится понятным, почему Кирилл Александрийский начал свою пасхалию ещё задолго до окончания действия пасхалии Феофила Александрийского: в своих пасхальных расчётах (и только!) он заменил эру Диоклетиана на эру Никейского собора. Причём для такой замены у Кирилла Александрийского определённо были свои причины. Чтобы разобраться в них, вспомним сначала, что в Вечном календаре длины пасхальных месяцев зависят от того, какое именно распределение длинных и коротких месяцев используется в данном календаре: при созигеновском распределении пасхальные месяцы имеют 29 или 30 дней, при альтернативном — только 30 дней, при средневековом — только 29 дней. Далее, как показано на Рис.4, к началу эры Диоклетиана (в 266–284 гг.) момент астрономического новолуния, усреднённый по всем месяцам «Вечного календаря Феофила Александрийского» (с альтернативным распределением месяцев), хотя и приходился на полночь в начале первых суток лунного месяца (линия 2), но, усреднённый только по 30-дневным (или только по пасхальным) месяцам цикла, он приходился на рассвет после этой полуночи (линия 4). А это определённо не соответствовало иудейскому счёту суток «от заката до заката». В эпоху же Никейского собора (в 323–341 гг.) в «Вечном календаре Кирилла Александрийского» (с созигеновским распределением месяцев) средний момент астрономического новолуния также приходился на полночь (линия 1). Однако в календаре Кирилла, в отличие от календаря Феофила, пасхальные месяцы имеют разные длины — 29 и 30 дней. Поэтому момент астрономического новолуния, усреднённый только по пасхальным месяцам календаря Кирилла, приходился на ту же полночь, что и усреднённый по всех месяцах этого календаря (а не на рассвет после этой полуночи, как в календаре Феофила). А это как раз и согласуется с иудейским счётом суток (см. главу 3).

Вернёмся теперь к заданному выше вопросу: почему средневековые пасхалисты изменили последовательность длинных и коротких месяцев в простых годах цикла? Дионисий Малый, которому было поручено продлить начиная с 532-го г. пасхалию Кирилла Александрийского, и его последователи, по-видимому, знали, что александрийский пасхальный цикл не совсем точный, и что реальные фазы Луны «спешат» по отношению к этому циклу на 1,47 часа за 19 лет (что уже обсуждалось в главе 2) или на одни сутки за 310 лет. Тогда можно предположить, что средневековые пасхалисты при продлении пасхалии решили не только сохранить александрийские даты пасхальных полнолуний, но и скомпенсировать среднюю по всем месяцам цикла сдвижку лунных фаз, набежавшую в «Вечном календаре Кирилла Александрийского» за 95 лет, т.е. за тот срок, на который была составлена соответствующая этому календарю пасхалия. Самое простое, что они могли сделать — это перенести на один день назад начала некоторого числа непасхальных 29-дневных месяцев в цикле. Чему же равно это число?

За 95 лет средний момент астрономического новолуния сдвигается в Вечном календаре назад на 95/310 частей суток. С другой стороны, если из 235-ти календарных лунных месяцев цикла выбрать один и перенести его начало на один день назад, то средний за цикл момент астрономического новолуния сдвинется в новом календаре вперёд на 1/235 часть суток. Поэтому число 29-дневных месяцев цикла, начала которых (для компенсации сдвижки лунных фаз за 95 лет) следует сдвинуть на один день назад, определяется соотношением: (95:310)×235 = 72. Совпадение этого числа с общим числом 29-дневных месяцев во всех простых годах цикла (12×6 = 72) приводит к очевидному решению: следует сдвинуть на один день назад начала всех 29-дневных месяцев во всех простых годах цикла или, что то же самое, изменить в простых годах цикла последовательность длинных и коротких месяцев. По-видимому, именно так и поступили средневековые пасхалисты — Дионисий Малый, Беда Достопочтенный и их последователи.

Как уже отмечалось, дошедшие до нас версии средневекового календаря несколько отличаются от таблицы 6. Например, начала месяцев в календаре, приведённом в книге М.Н. Лалоша [13, с.94–95], совпадают с таблицей 6 во всех случаях кроме восьми: четыре месяца начинаются на день раньше (исключения «со знаком минус») и четыре — на день позже (исключения «со знаком плюс»). Примечательно, что число исключений «со знаком минус» в точности равно числу исключений «со знаком плюс». Тот же самый «нулевой баланс» наблюдается и в календаре, приведённом в книге Ф.К. Гинцеля [14, с.136], хотя исключения там несколько другие. Заметим, что любые исключения с «нулевым балансом», введённые в средневековый календарь, не влияют на средний момент астрономического новолуния, вычисляемого в этом календаре. Поэтому все выводы, полученные из анализа привязки таблицы 6 к астрономическим фазам Луны, будут справедливыми и для версий средневекового календаря из книг М.Н. Лалоша и Ф.К. Гинцеля. Заметим также, что календарь, приведённый в книге И.А. Климишина [1, с.440], совпадает с календарём, приведённым в книге Ф.К. Гинцеля [14, с.136], за единственным исключением: второе новолуние августа в году с золотым числом G=8 у Климишина приходится на день позже, чем у Гинцеля. Скорее всего, это просто опечатка.

Изменение с годами среднего момента астрономического новолуния относительно начала лунного месяца в средневековом календаре показано на Рис.4 линией 3. На этом рисунке обращает на себя внимание следующая особенность: из-за разной последовательности длинных и коротких месяцев средние моменты астрономических новолуний в календарях Феофила Александрийского в 380 г. (линия 2), Кирилла Александрийского в 437 г. (линия 1) и Дионисия Малого в 532 г. (линия 3) приходились практически на одно и то же время последних суток лунного месяца (горизонтальная штрих-пунктирная линия). Получается, что каждый из этих трёх календарей в начале своего 95-летнего периода привязывался к одним и тем же фазам Луны. Однако подчеркнём, что в данном случае речь идёт о привязке календарей к моменту астрономического новолуния, усредняемому по всем месяцам цикла.

Далее, напомним, что во всех трёх вышеперечисленных календарях сохранены даты александрийских пасхальных полнолуний. Именно поэтому в каждом из этих календарей получается приблизительно одна и та же зависимость с годами среднего момента астрономического новолуния относительно начала лунного месяца, если усреднение проводить не по всем месяцам цикла, а только по месяцам той длины, которая может быть у пасхальных месяцев в данном рассматриваемом календаре. Действительно, на Рис.4 можно видеть ещё одну особенность: зависимости с годами средних моментов астрономических новолуний в 30-дневных месяцах календаря Феофила Александрийского (линия 4), во всех месяцах календаря Кирилла Александрийского (линия 1) и в 29-дневных месяцах календаря Дионисия Малого (линия 5) отличаются друг от другу незначительно.

Таким образом, рассматриваемый рисунок является иллюстрацией к тому, что именно сделали средневековые пасхалисты начиная с Дионисия Малого: для 532 г. они сохранили общую привязку календаря к лунным фазам, которая была у Феофила Александрийского в 380 г. и у Кирилла Александрийского в 437 г., но при этом сохранили ещё и даты александрийских пасхальных полнолуний.

Считается, что около 500 г. н.э. была завершена работа по созданию действующего вычисляемого иудейского календаря [1, с.258]. В этом календаре начало лунно-солнечного года определяется по алгоритму, основанному на математических действиях с многозначными цифрами. Однако реальное начало года по религиозным предписаниям примерно в 44% случаев сдвигается вперёд на один день, а примерно в 3% случаев — на два дня. Получается, что в этом календаре средний момент астрономического новолуния из-за предписаний сдвигается назад на полсуток. Так, в «календаре без предписаний» средний момент астрономического новолуния пасхальных месяцев приходится примерно на полночь в начале первых суток, а в календаре с предписаниями — на 12 часов раньше, т.е. примерно на полдень. Если же на Рис.4 продлить линию 5 назад до 500-го г., то видно, что календарь Дионисия Малого в начале VI в. как бы учитывает «иудейские предписания», но только в среднем и только для 29-дневных месяцев, включая все пасхальные.

При пасхальных расчётах были введены не только уже обсуждавшиеся великий индиктион и малый пасхальный круг, но и христианские эры от «сотворения мира». В основу многих из этих эр было положено соотношение между числом «дней творения мира» и продолжительностью его существования. Это соотношение было взято из Библии: «И сотворил Бог человека по образу Своему <...> И был вечер, и было утро: день шестой» (кн. Бытие, гл.1:27–31), «у Господа один день, как тысяча лет, и тысяча лет, как один день» (2-е послание Петра, гл.3:8). Ссылаясь на приведённые библейские утверждения, христианские богословы пришли к выводу, что поскольку «Адам был создан в середине шестого дня творения», то «Христос пришёл на Землю в середине шестого тысячелетия», т.е. около 5500 г. от «сотворения мира». Если разделить этот интервал лет на длину великого индиктиона: 5500:532 = 10,3, то получается, что «Христос пришёл на Землю в одиннадцатом великом индиктионе». Поэтому первым великим индиктионом, на полный срок которого следует составить пасхалию, может быть только двенадцатый. Далее идёт «естественное» требование: в самом конце 11-го великого индиктиона лунно-солнечный календарь привязывается к астрономическим фазам Луны должным образом и с максимально возможной точностью.

В первые века н.э. было придумано около 200 различных вариантов эры от «сотворения мира», среди которых важнейшими являются византийская (созданная в 353 г.) и александрийская (созданная около 400 г.) эры [1, с.327]. Летосчисление по византийской эре велось с субботы 1 сентября 5509 г. до н.э., а по александрийской — с 29 августа 5493 г. до н.э. Следовательно 12-й великий индиктион по византийской эре начался 1 сентября 344 г., а по александрийской — 29 августа 360 г. (в обоих случаях через 11×532 = 5852 года от «сотворения мира»). Великий индиктион по определению должен начинаться вместе с 19-летним циклом. Действительно, 345 г. — это год с кругом Луны L=1, а 361 г. — это год c золотым числом G=1. Поэтому, если великий индиктион начинать не осенью, а в январе и обязательно в год с золотым числом равным единице, то началом 12-го великого индиктиона (так как G = L+3) будет 345−3 = 342 г. по византийской эре и 361 г. по александрийской.

Таким образом, если в византийской эре перейти на золотое число, то получается, что пасхалия Кирилла Александрийского была составлена на второе 95-летие 12-го великого индиктиона этой эры, а пасхалия Дионисия Малого — на третье. Но почему в византийской эре вместо золотого числа стали использовать круг Луны? Дело в том, что при императоре Диоклетиане в Римской империи каждые 15 лет проводилась переоценка имущества с целью установления величины налогов. Поэтому стали считать индикты — порядковые номера годов в каждом 15-летнем промежутке, а в 312 г. при императоре Константине это счисление было введено официально, причём счёт начинался с 23 сентября. В Византии в 462 г. из практических соображений начало года и отсчёта индиктов было перенесено на 1 сентября [1, с.126]. Создатели византийской эры решили, что в первый год от «сотворения мира» должны начинаться сразу все три цикла: 19-летний лунный, 28-летний солнечный и 15-летний индиктовый циклы. Замена золотого числа на круг Луны и была сделана для того, чтобы удовлетворить этому условию. В VI в. начало византийской эры было перенесено на полгода вперёд, т.е. на пятницу 1 марта 5508 г. до н.э. Эта эра известна под названием константинопольская (а также древнерусская) эра «от Адама», так как она началась в пятницу — в шестой «день творения», когда «был сотворён» Адам. В Византии эра от «сотворения мира» с началом 1 сентября 5509 г. до н.э. была официально утверждена на VI Вселенском соборе (681 г.).

Как уже отмечалось, в 323–341 гг. (в то 19-летие, в котором состоялся Никейский собор) средний момент астрономического новолуния в Вечном календаре с созигеновским распределением длинных и коротких месяцев приходился на полночь по александрийскому времени в начале первых суток лунного месяца, что относится к усреднению как по всем месяцам цикла, так и только по пасхальным. Такую привязку для данного календаря можно назвать «началом» календаря. Таким образом, последнее 19-летие 11-го великого индиктиона по византийской эре от «сотворения мира» является «началом» Вечного календаря с созигеновским распределением месяцев, а начало 12-го великого индиктиона по этой же эре совпадает с началом эры Никейского собора.

Казалось бы, что 12-й великий индиктион по александрийской эре от «сотворения мира» должен начинаться в 285 г. вместе с эрой Диоклетиана. Но, как уже было сказано, он начинается в 361 г., через 76 лет после начала эры Диоклетиана. Это связано с тем, что в 266–284 гг. привязка к лунным фазам Вечного календаря с альтернативным распределением месяцев не была оптимальной: хотя средний момент астрономического новолуния и приходился на полночь в начале первых суток лунного месяца, но, усреднённый только по 30-дневным (или только по пасхальным) месяцам цикла, он приходился на 6 часов позже (см. линии 2 и 4 на Рис.4). Однако через 76 лет средний момент астрономического новолуния в этом календаре из-за погрешности цикла сместился назад примерно на 6 часов и привязка календаря к лунным фазам стала оптимальной. Действительно, расчёт показывает, что в 342–360 гг. момент астрономического новолуния, усреднённый в рассматриваемом календаре только по 30-дневным (или только по пасхальным) месяцам цикла, пришёлся на полночь в начале первых суток лунного месяца, а точнее на 0 час 20 мин по александрийскому времени. Поэтому 19-летие с 342-го по 360-й гг., являющееся последним 19-летием 11-го великого индиктиона по александрийской эре от «сотворения мира», можно назвать «началом» Вечного календаря с альтернативным распределением месяцев.

Подводя итоги данной главы, следует в первую очередь отметить, что изменение последовательности длинных и коротких месяцев в «Вечном лунно-солнечном календаре» служило, по-видимому, одним из способов привязки этого календаря к лунным фазам. Результаты приведённых в этой же главе расчётов, касающиеся христианских эр от «сотворения мира», можно кратко изложить следующим образом: если предположить, что в IV–VII вв.

6. Датировка библейской Тайной вечери

Древняя проблема датировки Тайной вечери заключается в следующем. С одной стороны, все четыре библейских евангелиста единогласно утверждают, что Иисус Христос был распят в пятницу (Матфей, гл.27:62; Марк, гл.15:42; Лука, гл.23:54; Иоанн, гл.19:14), а Тайная вечеря состоялась накануне — вечером с четверга на пятницу. С другой стороны, из слов первых трёх евангелистов следует, что Тайная вечеря была именно ветхозаветной пасхальной трапезой: «В первый день опресноков, когда заколали пасхального агнца, говорят Ему ученики Его: где хочешь есть пасху? мы пойдём и приготовим» (Матфей, гл.26:17; Марк, гл.14:12; Лука, гл.22:7–9), а четвёртый евангелист определённо утверждает, что в день распятия «была пятница перед Пасхою» (Иоанн, гл. 18:28, 19:14, 19:31), из чего следует, что Тайная вечеря ветхозаветной пасхальной трапезой не была.

В своих рассказах о Тайной вечери ни один из евангелистов не называет никаких календарных дат, но согласно Библии ветхозаветная пасха совершается «в первый месяц, в четырнадцатый [день] месяца вечером» (кн. Левит, гл.23:5). Поэтому из слов Матфея, Марка и Луки следует, что Тайная вечеря состоялась вечером с 14-го нисана на 15-е, а из слов Иоанна — с 13-го на 14-е. Существует несколько гипотез, объясняющих это как бы разногласие. Согласно одной из них (так называемой гипотезе о двух разных календарях) Иоанн пользовался религиозным календарём Иерусалимского храма, а Матфей, Марк и Лука — другим календарём. Говоря об этом «другом календаре», обычно противопоставляют (см., например, книгу [15, с.43–44]) календари саддукеев и фарисеев (религиозных сект в иудаизме) или календари Иудеи и Галилеи (областей в Палестине, в каждой из которых во времена Страстей Христовых был свой назначаемый Римом правитель).

После завоевания персидскими царями в VI в. до н.э. Вавилона во всей Персидской империи для официального государственного делопроизводства был принят вавилонский лунно-солнечный календарь (хотя наряду с вавилонским сохранялись и местные календари). В Сирийском царстве, образовавшемся в конце IV в. до н.э. после завоеваний Александра Македонского и включавшем часть территорий, входивших ранее в состав Персидской империи, «сирийские» (вавилонские) названия месяцев были заменены на македонские [3, с.21] (такой календарь называют сирийско-македонским). Что касается Палестины, то она вместе со своими северными соседями входила в состав как Персидской империи, так и Сирийского царства. В 62 г. до н.э., за 16 лет до юлианской календарной реформы, Сирия становится римской провинцией, а Иудея теряет свою независимость, завоёванную в середине II в. до н.э.: её правитель и первосвященник назначается Римом [3, с.277].

Напомним, что начиная с конца IV в. до н.э. в вавилонском лунно-солнечном календаре стал использоваться 19-летний цикл, а также, что при реконструкции цезаревского календаря (см. вторую главу) получился тот же самый 19-летний цикл, который известен как сирийский, а также как иудейский. Напрашивается естественное предположение, что при проведении юлианской календарной реформы в некоторых или даже во многих сирийских городах дни новолуний местного сирийско-македонского календаря (для удобства перевода дат юлианского календаря Римской империи в местный провинциальный и наоборот) были расписаны в юлианском календаре по тем же самым принципам, что и при реконструкции гипотетического цезаревского календаря. То же самое предположение можно отнести и к проведению юлианской календарной реформы в Иудее, которая в 6 г. н.э. была сделана римской провинцией [3, с.284]. Там один из вариантов сирийско-македонского календаря использовался в качестве местного гражданского календаря (Э. Бикерман называет его «официальным "непогрешимым" календарём Иерусалимского храма» [3, с.22]). Например, иудейский историк I в. н.э. Иосиф Флавий, датируя описываемые в своих книгах события, называет не иудейские, а македонские месяцы ксантик [16, с.479], гарпей [с.614], артемизий [с.321] и другие. Поэтому не исключено, что после календарной реформы этим «гражданским календарём» был именно цезаревский (адаптированный сирийско-македонский) календарь, введённый в Иудее в честь Цезаря (подобно тому, как в Палестине на рубеже н.э. в честь римских императоров назывались целые города: Цезария [17, с.316], Себаста [с.393], Тивериада [с.435] и другие).

Учитывая все факты, изложенные в настоящей статье, можно предложить следующую гипотезу: евангелисты Матфей, Марк и Лука при описании Тайной вечери основывались именно на местном гражданском лунно-солнечном календаре, в качестве которого использовался цезаревский календарь.

Однако, поскольку речь идёт о ветхозаветной пасхе, необходимо проверить, что в описанную евангелистами эпоху цезаревский календарь был должным образом привязан к фазам Луны. Как уже многократно отмечалось, для цезаревского календаря, в котором пасхальные месяцы имеют как 30, так и 29 дней, оптимальной («идеальной» для пасхальных вычислений) привязкой является такая привязка, при которой средний момент астрономического новолуния приходится на полночь в начале первых суток лунного месяца. Так как в 58–40 гг. до н.э. этот момент (см. главу 2) приходился по александрийскому времени на 6 час 9 мин первых суток месяца, то спустя четыре 19-летних периода (4×19 = 76 лет) он из-за погрешности цикла стал приходиться примерно на 6 часов раньше, т.е. на полночь. Таким образом, в 19–37 гг. н.э. цезаревский календарь действительно был оптимально привязан к фазам Луны и, следовательно, вполне мог использоваться для определения дат ветхозаветной пасхи. Но именно на это же 19-летие приходилось и правление римского наместника (прокуратора) Понтия Пилата. Как известно, он правил в Иудее с 26-го по 36-й гг. н.э. [3, с.285–286] и в его правление был распят Иисус Христос (Матфей, гл.27:2; Марк, гл.15:1; Лука, гл.23:1; Иоанн, гл.18:29).

Теперь осталось определить, в каком конкретно году за время правления Понтия Пилата ветхозаветная пасха, вычисленная по цезаревскому календарю, приходилась именно на четверг — на тот день недели, на который, согласно евангелистам, пришлась Тайная вечеря. С этой целью в таблице 7 для интервала лет с 26-го по 36-й гг. н.э. и для разных лунно-солнечных календарей приведены юлианские даты ветхозаветной пасхи, т.е. даты пасхальных полнолуний или 14-го нисана, и соответствующие им дни недели. В этой же таблице для сравнения приведены также соответствующие годы летосчисления по Олимпиадам (столбец Ol.) и годы царствования римского императора Тиберия (столбец Т.). Примечательно, что ветхозаветная пасха по цезаревскому календарю (столбец ЦК) только один раз за все годы правления Понтия Пилата, а именно в 33-м г. н.э., приходилась на четверг.

Таблица 7 Даты пасхальных полнолуний в разных календарях за период, когда Понтий Пилат был наместником (прокуратором) Иудеи, т.е. с 26-го по 36-й гг. н.э.
Обозначения: н.э. — год нашего летосчисления; Ol. — год летосчисления по Олимпиадам; Т. — год царствования римского императора Тиберия; ЦК — пасхальное полнолуние в цезаревском календаре; а.в.Л. — астрономический возраст Луны (в часах) на закате во время «расчётной неомении» пасхального месяца; 14Д — дата вечера на исходе 14-го дня пасхального месяца, начинающегося в «расчётную неомению», т.е. на закате при возрасте Луны от 16,5 до 40,5 часов; ППП и КПП — православное и католическое пасхальные полнолуния; ИПП — 14-е нисана в иудейском вычисляемом календаре без предписанных сдвижек. Все даты указаны по ст.ст., при составлении столбцов а.в.Л. и 14Д использовалось иерусалимское время и требовалось, чтобы пасхальное полнолуние было первым после весеннего равноденствия.

Таким образом, согласно предложенной гипотезе о роли цезаревского календаря, Тайная вечеря — последняя трапеза Иисуса Христа с апостолами — состоялась 2-го апреля по ст.ст. 33-го г. н.э.

Дополнительно в таблице 7 приведены юлианские даты пасхальных полнолуний в православной (столбец ППП) и католической (столбец КПП) пасхалиях, а также юлианские даты 14-го нисана в вычисляемом иудейском календаре без предписанных сдвижек (столбец ИПП). Эти даты получены экстраполированием назад известных пасхалий, которые, однако, были составлены значительно позже периода правления Понтия Пилата. Поэтому они интересны только для сравнения, так как в прошлом не раз предпринимались попытки датировать первую христианскую Пасху именно по этим пасхалиям.

А вот дополнительный столбец 14Д в таблице 7 действительно представляет определённый интерес, несмотря на то, что подобные расчёты были выполнены ещё в XVIII в. английским учёным Исааком Ньютоном, открывшим физические законы, носящие его имя [18, с.301–304]. В этом столбце приведены юлианские даты «пасхальных полнолуний», определённых не по какому-либо календарному расписанию, а с использованием моментов времени астрономических новолуний, вычисленных по уже упомянутым формулам [5, 6]. Дата такого «пасхального полнолуния» — это дата вечера на исходе 14-го дня пасхального месяца при условии, что а) этот месяц начался в «расчётную неомению», т.е. на закате в 18 часов по иерусалимскому времени при астрономическом возрасте Луны от 16,5 до 16,5+24 = 40,5 часов (этот возраст приведён в столбце а.в.Л.), и что б) определённое таким образом «пасхальное полнолуние» является первым после весеннего равноденствия. Возраст Луны во время неомении взят из книг Э. Бикермана [3, с.15] и И.А. Климишина [1, с.68], в которых утверждается, что в марте на широте Вавилона (близкой к широте Иерусалима) промежуток времени между астрономическим новолунием и неоменией составляет не менее 16,5 часов.

Другими словами, в столбце 14Д таблицы 7 приведены юлианские даты ветхозаветной пасхи (14-го нисана) в таком лунно-солнечном календаре, в котором начало 1-го дня пасхального месяца определялось как бы с помощью наблюдения неомении при благоприятных погодных условиях. Заметим, однако, что этот календарь в некоторых случаях может и не совпадать с историческим религиозным календарём Иерусалимского храма первой половины I в. н.э., так как в то время реальные погодные условия влияли как на наблюдение неомении, так и на вставку эмболисмического месяца.

Из таблицы 7 видно, что 14-е нисана по календарю, определяемому «расчётной неоменией» (столбец 14Д), пришлось на пятницу (день Распятия) только один раз за весь период правления Понтия Пилата, причём на пятницу именно того года, в котором 14-е нисана по цезаревскому календарю (столбец ЦК) пришлось на четверг (день Тайной вечери). Что же касается исторического религиозного календаря Иерусалимского храма, то 14-е нисана в этом календаре могло выпасть на пятницу ещё и в 27-м и 30-м гг., если в эти годы из-за неблагоприятных для наблюдения неомении погодных условий начало пасхального месяца было перенесено на один день позже.

Исходя из этих расчётов, а также из гипотезы о цезаревском календаре, можно предложить следующее объяснение кажущегося разногласия между евангелистами относительно датировки Тайной вечери: евангелист Иоанн в своём рассказе использовал «религиозный календарь Иерусалимского храма», в котором начала лунных месяцев определялись по наблюдениям неомении и в котором вечер с 14-го на 15-е нисана пришёлся на пятницу 3-го апреля 33 г., а евангелисты Матфей, Марк и Лука в своих рассказах использовали «официальный гражданский календарь», совпадающий с цезаревским, в котором начала лунных месяцев были привязаны к расчётному астрономическому новолунию и в котором вечер с 14-го на 15-е нисана пришёлся на четверг 2-го апреля 33 г. Из этого объяснения следует, что Христос был распят 3-го апреля 33 г. — в тот самый день и час, когда в Иерусалимском храме приносились пасхальные жертвы, а Тайная вечеря состоялась 2-го апреля, когда Христос и апостолы отмечали ветхозаветную пасху по календарю, определяемому истинным (астрономическим) новолунием.

Отметим также, что кажущееся противоречие между евангелистами относительно датировки Тайной вечери является, по-видимому, отражением календарной проблемы той эпохи, а именно вопроса: как начинать лунный месяц — в первое наблюдаемое новолуние или в расчётное истинное.

По-видимому, с подобной же проблемой связан и следующий исторический факт. Церковный историк Беда Достопочтенный утверждает, что «в году от воплощения Господа 664-м» на соборе в монастыре под названием Стренескальк (Витби, Англия) «возник великий и вовлекший многих спор о праздновании Пасхи», показавший, что исчисление ирландцами пасхального воскресенья «расходится с обычаями Вселенской Церкви». Суть данного спора заключалась в том, что римлянами пасхальное воскресенье отмечалось «между 15-м и 21-м днями луны», а ирландцами — «между 14-м и 20-м днями» [19, с.100–104]. Согласно пасхалии Дионисия Малого, которая в 532 г. была принята и в Риме, христианская Пасха должна отмечаться в первое воскресенье после пасхи ветхозаветной, т.е. после вечера с 14-го на 15-е нисана. Именно поэтому пасхальное воскресенье должно попадать «между 15-м и 21-м днями луны», а не «между 14-м и 20-м днями». Тем не менее, ирландцев также можно понять, если предположить, что в то время, когда был спор о Пасхе, их лунный месяц начинался на один день раньше, чем месяц в календаре Дионисия Малого. При таком предположении получается, что ирландцы отмечали пасхальное воскресенье «правильно» — «между 15-м и 21-м днями луны», однако отмечали по своему календарю. Но тогда почему же лунный месяц ирландцев мог начинаться на один день раньше?

Напомним, что Дионисий Малый в своём календаре сохранил александрийские пасхальные новолуния (новолуния пасхальных месяцев), которые были оптимально привязаны к астрономическим фазам Луны эпохи Никейского собора. Однако через 310 лет после Никейского собора, но за 29 лет до собора в Витби, на котором произошёл спор о Пасхе, пасхальные новолуния Дионисия Малого из-за погрешности цикла стали запаздывать в среднем на одни сутки по отношения к реальным астрономическим новолуниям. Возможно, ирландские пасхалисты просто ввели лунную поправку, чтобы их лунный месяц был бы так же оптимально привязан к астрономическому новолунию, как это было у александрийцев в эпоху Никейского собора. Но тогда почему такую же поправку не ввели и в александрийской пасхалии?

Ко времени составления Дионисием Малым своей пасхалии отцы церкви уже решили в основном вопрос, связанный с проблемой датировки Тайной вечери, а именно вопрос: был ли Христос распят 15-го нисана, как это следует из рассказов евангелистов Матфея, Марка и Луки, или 14-го нисана, как это следует из рассказа евангелиста Иоанна. Дату распятия Христа определили по Иоанну — 14-е нисана, «ибо Пасха наша, Христос, заклан за нас» (Библия, 1-е послание к коринфянам св. апостола Павла, гл.5:7), а пасхальные жертвоприношения совершаются «в первый месяц, в четырнадцатый [день] месяца вечером». В связи с этим решением необходимо было также «по Иоанну» привязать к фазам Луны и расписание пасхальных новолуний. Поскольку в эпоху Никейского собора александрийское расписание пасхальных новолуний было оптимально привязано именно к астрономическим новолуниям (см. главу 4), то эту привязку (в рамках гипотезы, предложенной в настоящей главе и объясняющей разногласие между евангелистами относительно датировки Тайной вечери) можно назвать привязкой «по Матфею, Марку и Луке». Однако три века спустя, когда астрономические новолуния из-за погрешности цикла стали опережать календарные в среднем на одни сутки, привязка александрийских пасхальных новолуний к фазам Луны становится привязкой к первым наблюдаемым новолуниям или привязкой «по Иоанну». Таким образом, в VII в. пасхальные новолуния Дионисия Малого (они же александрийские) автоматически уже были привязаны к фазам Луны именно «по Иоанну» и никаких дополнительных лунных поправок не требовалось.

Далее отметим, что в рамках предложенной гипотезы, объясняющей с помощью цезаревского календаря проблему датировки Тайной вечери, год распятия Христа вычисляется однозначно. Этот год совпадает с датировкой, приведённой в «Хронике» Евсевия Кесарийского (ок. 260–340 гг.): «Христос был распят и воскрес на 19-м году правления Тиберия, или на 4-м году 202-й Олимпиады» [1, с.337]. Датировка по годам правления римского императора Тиберия основывается на свидетельстве евангелиста Луки, что Иоанн Креститель начал проповедовать крещение «в пятнадцатый же год правления Тиверия кесаря» (Лука, гл.3:1–2), а также на собственных расчётах Евсевия, что после крещения у Иоанна «время учительства Спасителя нашего продолжалось неполных четыре года» [9, с.39]. Датировка по Олимпиадам, приведённая Евсевием, появилась в первой половине II в. благодаря исторической хронике «Выдержки из Олимпиад» греческого языческого писателя Флегона [20, с.36–40], утверждавшего (в пересказе христианских писателей), что в 4-м году 202-й Олимпиады было сильное землетрясение в Вифинии, разрушевшее много зданий в Никее, и необычайное «затмение солнца», начавшееся в полдень (необычайное — потому, что оно случилось во время полнолуния). Евсевий нашёл свидетельство Флегона согласующимся как с его собственной датировкой, так и с евангельскими рассказами, что во время распятия Христа «и померкло солнце» (Лука, гл.23:45), «и земля потряслась» (Матфей, гл.27:51).

Приводя свидетельство Флегона, необходимо сделать следующее замечание. Христианский теолог и писатель Ориген (185–254 гг.) в своём трактате «Против Цельса» (кн.II, гл.14) пишет: «Флегон <...> приписал Христу предвидение неведомого будущего. Правда, он перепутал и вместо того, чтобы говорить об Иисусе, говорит о Петре, но он всё же засвидетельствовал, что исполнилось всё, что и как Он предсказал» [20, с.36]. Возможно, что в этом отрывке речь идёт об апостоле Петре, который в 50-й день после первой христианской Пасхи напомнил предсказания ветхозаветного пророка Иоиля (Деяния св. апостолов, гл.2:14–21), среди которых есть и такие слова: «Солнце превратится во тьму и луна — в кровь, прежде нежели наступит день Господень...» (кн. пророка Иоиля, гл.2:31). Если это действительно так, то Флегон определённо связывает дату «землетрясения и затмения» с датой распятия Христа. Однако, раннехристианские богословы понимали, что обычное солнечное затмение не могло быть в канун иудейской пасхи (а именно тогда распяли Христа), так как этот праздник отмечается в дни полнолуния, когда Луна и Солнце находятся в оппозиции. А вот лунное затмение, про которое в древности говорили, что «луна превращается в кровь», вполне могло быть в день распятия Христа. Поэтому возможно, что два разных события — «помрачение солнца в полдень» и «лунное затмение на закате» — Флегон перепутал с одним «солнечным затмением».

Это предположение удивительным образом согласуется с астрономическими расчётами (см., например, [5]), согласно которым в пятницу 3-го апреля по ст.ст. 4-го года 202-й Олимпиады (33-го г. н.э.) произошло частное лунное затмение, которое началось примерно за 2,4 часа до восхода Луны в Иерусалиме, а закончилось примерно через полчаса после этого восхода. Однако надо сказать, что во время частных лунных затмений «покраснение» затемнённой части лунного диска практически не наблюдается на фоне яркой незатемнённой части. Поэтому не исключено, что сообщение Флегона о затмении (если речь идёт действительно о лунном затмении) основывается не на свидетельствах очевидцев, а только на астрономических расчётах того времени.

Добавим, что по нашему летосчислению 19-й год царствования императора Тиберия продолжался с августа 32-го по август 33-го гг. [3, с.285, 236], а 4-й год 202-й Олимпиады — с июня 32-го по июнь 33-го гг. [3, с.172]. Датировка распятия Христа 33-м годом н.э. получила дальнейшее распространение в хрониках византийского историка Георгия Синкелла (рубеж VIII–IX вв.) и антиохийского патриарха Михаила Сирийца (1126–1199 гг.). Этим же самым годом распятие Христа датируется и в «Англосаксонских хрониках» (период до 750 г.), записанных в конце IX в. на основе «Истории» Беды Достопочтенного (673–735 гг.) [19, с.221].

7. Заключение

Логическим следствием гипотезы «о цезаревском лунно-солнечном календаре и о его дальнейшей модификации» — об оборотной стороне календарной реформы Юлия Цезаря, подробно изложенной в настоящей статье, являются следующие исторически известные календарные характеристики:

В рамках этой гипотезы кажущееся противоречие между рассказами библейских евангелистов относительно датировки Тайной вечери объясняется тем, что начало лунного месяца у евангелиста Иоанна определяется по первому наблюдаемому новолунию, а у евангелистов Матфея, Марка и Луки — по астрономическому новолунию, вычисляемому по цезаревскому лунно-солнечному календарю. Другими словами, в первом случае использовался религиозный календарь Иерусалимского храма, а во втором — официальный гражданский календарь. Кроме того, эта гипотеза не только объясняет рассмотренное противоречие, но и приводит к однозначной датировке распятия Христа, совпадающей с древней датировкой Флегона, известной ещё в первой половине II в. н.э.

Символично, что в цезаревском календаре в эпоху Страстей Христовых, а также в его модифицированном варианте (т.е. в предполагаемом прообразе вычисляемого иудейского календаря) в эпоху разрушения Иерусалимского храма средний момент астрономического новолуния приходился практически на начало первых суток лунного месяца, если в первом календаре началом суток считать полночь, как потом стало у христиан, а во втором — закат — традиционное начало суток у иудеев.

Таким образом, есть все основания утверждать, что гипотеза о цезаревском календаре и объяснение с её помощью противоречия в датировках Тайной вечери имеют достаточно высокую степень вероятности.

Оглавление

Владимир Уваров

Оборотная стороная календарной реформы Юлия Цезаря

Cм. Мф 26:17

См. библиографию. Cм. обзор Меня.

Автор о себе:

1. Введение

2. Первичное расписание новолуний в юлианском календаре

3. Альтернативное расписание новолуний в юлианском календаре для эпохи разрушения Иерусалимского храма

4. Расписание пасхальных полнолуний в юлианском календаре

5. Средневековый лунно-солнечный церковный календарь и христианские эры от «сотворения мира»

6. Датировка библейской Тайной вечери

7. Заключение

Литература:

См.: История человечества - Человек - Вера - Христос - Свобода - На первую страницу (указатели).

Внимание: если кликнуть на картинку
в самом верху страницы со словами
«Яков Кротов. Опыты»,
то вы окажетесь в основном оглавлении.

Оглавление

Владимир Уваров

Оборотная стороная календарной реформы Юлия Цезаря

Cм. Мф 26:17

См. библиографию. Cм. обзор Меня.

Автор о себе:

1. Введение

2. Первичное расписание новолуний в юлианском календаре

3. Альтернативное расписание новолуний в юлианском календаре для эпохи разрушения Иерусалимского храма

4. Расписание пасхальных полнолуний в юлианском календаре

5. Средневековый лунно-солнечный церковный календарь и христианские эры от «сотворения мира»

6. Датировка библейской Тайной вечери

7. Заключение

Литература:

См.: История человечества - Человек - Вера - Христос - Свобода - На первую страницу (указатели).

Внимание: если кликнуть на картинку в самом верху страницы со словами «Яков Кротов. Опыты», то вы окажетесь в основном оглавлении.

Внимание: если кликнуть на картинку
в самом верху страницы со словами
«Яков Кротов. Опыты»,
то вы окажетесь в основном оглавлении.